The main concept behind the nodal analysis is that , in a given circuit if the node voltages are known, then we can immediately determine all branch currents associated with the circuit. As we know that , for finding node voltages we use KCL. In this technique, node voltages are considered as variables in the circuit , instead of element voltages , which results in reduction of the number of equations to simplify the circuit. In nodal analysis method , with availability of all the nodes, one node is considered as a reference node (zero potential) and it is represented as ground terminal. To other remaining unknown nodes , voltages are assigned , with respect to the referenced node voltage.
To the each node in a given circuit, we apply the KCL except for the referenced node. Suppose if the given circuit has N nodes, then we get N-1 simultaneous equations to find the N-1 unknown node voltages.
Outline
ToggleSteps to Analyse Nodal Analysis Technique
1) Check the possibility to transform voltage sources in the given circuit to the current sources and transform them.
2) Identify the nodes present in the given circuit and assign one node as reference node and with respect to this ground or reference node , label other nodes as unknown node voltages.
3) Assign the current direction in each branch in the given circuit (it is an arbitrary decision).
4) Apply KCL to N-1 nodes and write nodal equations by expressing the branch currents as node assigned voltages.
5) Solve the simultaneous equations of nodes to find the node voltages and finally branch currents. The number of node equations is equal to the number of nodes minus one (as one node is referenced).
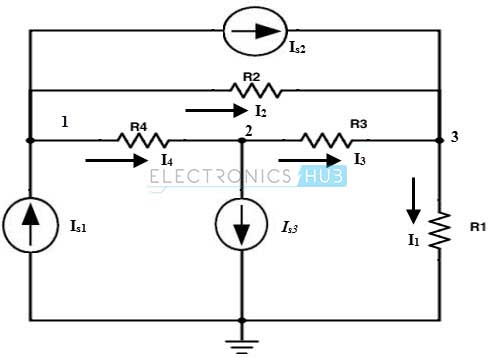
Consider below DC circuit, in which branch currents are to be determined using the nodal analysis.
As a first step in nodal analysis, we have to select the reference node which is to be connected to the zero or ground potential as indicated below.
Secondly, we apply Kirchoff’s Current Law (KCL) to each node in the circuit except the reference node. By applying KCL at node 1 we get,
Is1 – Is3 – I4 – I2 = 0
Is1 – Is3 – {(V1 – V2)/R4} – {(V1- V3)/R2} = 0
Is1 – Is3 = V1 { (1/R2) + (1/R4)} – V2 (1/R4) – V3 (1/R2)
Is1- Is3 = G11 V1 – G12 V2 – G13 V3 ………………………..(1)
where , G1i is the sum of total conductance at the first node. (As we know that 1/ R = G)
By applying KCL at node 2 we get
I4 – Is2 – I3 = 0
{(V1 – V2)/R4} – Is2 – {(V2 – V3)/R3} = 0
– Is2 = – V1 (1/R4) + V2 { (1/R3) + (1/R4)} – V3 (1/R3)
– Is2 = – G21 V1 – G22 V2 – G23 V3 ……………………………(2)
Applying KCL at node 3 we get
Is3 + I2 + I3 – I1 = 0
Is3 + {(V1 – V3)/R2} – {(V2 – V3)/R3}– V3 (1/R1) = 0
Is3 = – V1 (1/R2) – V2 (1/R3) + V3 { (1/R1) + (1/R2) + (1/R3)}
Is3 = – G31 V1 – G32 V2 + G33 V3…………………………..(3)
Likewise, we can write the KCL equations for i th node. And hence
∑ Iii is equal to the algebraic sum of all the currents connected at the i th node where i = 1, 2, 3……N and N = n-1 (n is the total number of nodes present in the circuit).
Gii = The sum of conductance connected to the i th node.
Gij = The sum of conductance connected between i and j nodes.
By solving the above three equations we get the branch voltages at respective nodes and thereby we can calculate branch currents.
Example
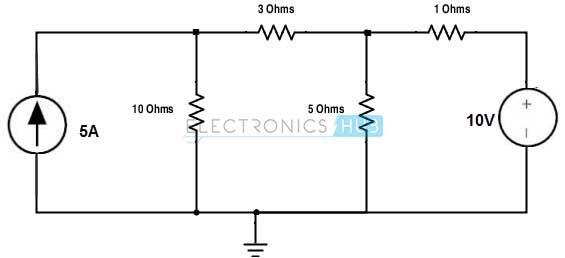
Determine the node voltages and currents in each branch using nodal analysis method in the given circuit.
The given circuit contains a voltage source. This can be transformed to current source or can be analysed directly without any transformation. Now let us calculate the nodal voltages without any transformation.
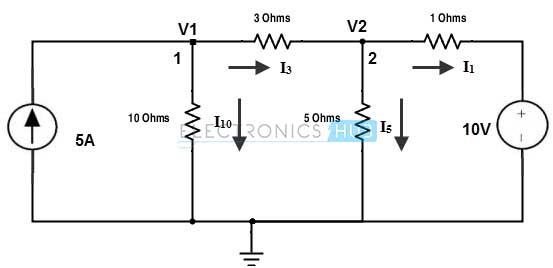
As a first step in nodal analysis, we have to choose and label the nodes present in the given circuit. By choosing the bottom node as reference node, we have two another nodes in the given circuit. So these nodes are labelled as V1 and V2 as shown in below figure. And also current directions in each branch are represented.
By applying KCL at node 1, we get
5 = I3 + I10
5 = (V1/10) + (V1 – V2/3)
13V1 – 10V2 = 150 ………(1)
By applying KCL at node 2, we get
I3 = I5 + I1
(V1 – V2/3) = (V2/5) + (V2 – 10/1)
5V1 – 23V2 = -150 ……..(2)
By solving above two equations, we get
V1 = 19.85 Volts and V2 = 10.9 Volts
The currents in each branch is given as
I10 = V1/10
= 19.85/10 = 1.985
I3 = V1 – V2/3
= 19.85 – 10.9/3
= 2.98 A
I5 = V2/5
= 10.9/5
= 2.18 A
I1 = V2 – 10
= 10.9 – 10
= 0.9 A
Concept of Supernode
Sometimes it becomes difficult to apply nodal analysis when any voltage source is present in between two branches in a circuit. One way to overcome this problem is by applying a super node technique. In super node technique, voltage source is connected between two adjacent nodes is shorted to reduce the two nodes to form a single super node.
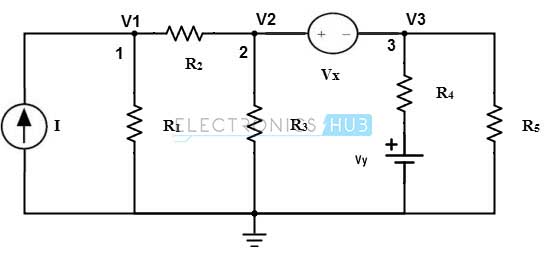
Consider the above example in which a voltage source is connected between the 2 and 3 nodes. The calculations become more difficult if we analyse the circuit with voltage source. The analysis of this circuit becomes easier if we create a super node by shorting 2 and 3 nodes.
By applying kirchoff’s current law at the node 1 we get,
I = (V1/R1) + ((V1-V2)/R2) ……(1)
The super node technique can be applied to the given circuit by shorting the 2 and 3 nodes and by applying KCL we get
((V2-V1)/R2) + (V2/R3) + ((V3-Vy)/R4) + (V3/R5) = 0
And also voltage in the voltage source is given as
Vx = V2 – V3
From the above three equations, we can easily find out the three unknown voltages in the circuit.
Example of Super node
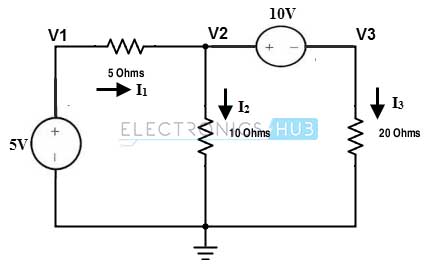
Consider the below circuit and find the three unknown node voltages V1, V2 and V3 by using super node technique.
At node 1, source is connected to the reference node and hence V1 becomes 5v
V1 = 5 V
A super node is formed by enclosing the nodes 2 and 3. By applying KCL at this super node we get
i1 = i2 + i3
(V1 – V2)/5 = (V2 / 10) + (V3/20)……………..(1)
And also KVL at super node gives,
V2 – V3 = 10…………… (2)
By solving above equations, we get V2 = 4.29V and V3 = -5.71 V