Two resistors are said to be connected in parallel if both the terminals of a resistor are connected to each respective terminal of other resistor. In a network of parallel resistors, current can take more than one path unlike in series resistor network as there are multiple paths for the current to flow. Hence parallel resistor circuits are current dividers.
Outline
ToggleResistors in Parallel
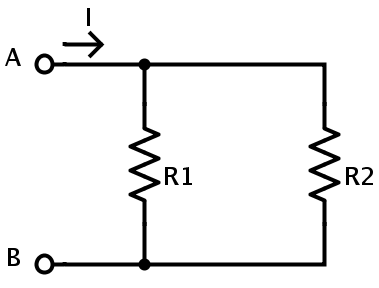
If two or more resistors are connected in parallel, then the potential difference across each resistor is same. Resistors in parallel connection are connected to the same nodes. This can be identified by the presence of more than one path for the current to flow. For example, the circuit shown below is a parallel connection of resistors. The potential difference across the resistor R1 is same as that across the resistor R2 which is equal to the supply potential VAB.
If VAB is the potential supplied then
VR1 = VR2 = VAB
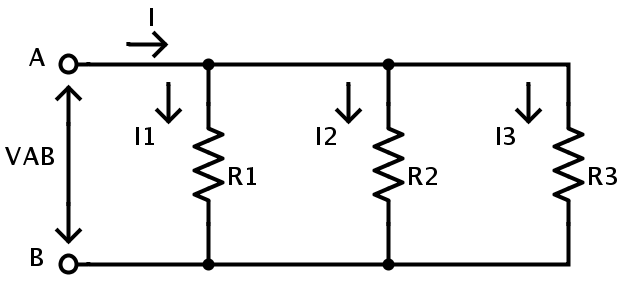
In the following circuit, the resistors R1, R2 and R3 are connected in parallel combination.
Here the supply potential is VAB between the points A and B. Since the resistors R1, R2 and R3 are connected in parallel combination the potential difference across each resistor is same as the supply. Hence VAB = VR1 = VR2 = VR3.
Where
VR1 is the potential across the resistor R1.
VR2 is the potential across the resistor R2.
VR3 is the potential across the resistor R3.
But the current flowing through these three resistors is different. If I is the current leaving the node A then it has three paths to reach the node B. The current flowing through each resistor is dependent on its resistance. Hence in case of parallel resistive circuits, the current is not same in all the resistors. If I1 is the current flowing through the resistor R1, I2 is the current flowing through the resistor R2 and I3 is the current flowing through the resistor R3 then the currents I, I1, I2 and I3 can be related with the help of Kirchhoff’s Current Law. According to Kirchhoff’s Current Law, “the sum of currents entering a node is equal to the sum of currents leaving the node.”
Hence
I = I1 + I2 + I3.
Equivalent resistance Formula
Any number of resistors connected in a parallel combination can be replaced by a single resistor with the resistance equal to the equivalent resistance of the parallel combination resistors.
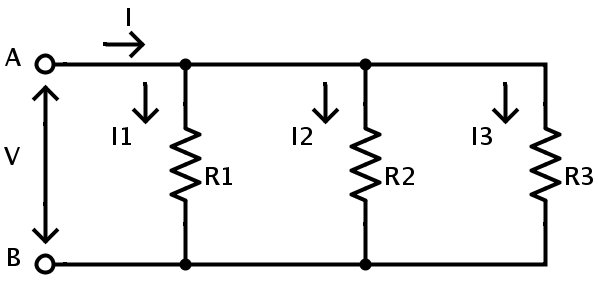
It has been established that the voltage across each resistor in a parallel combination is same and the total current is equal to sum of individual currents. Consider the following circuit.
Here, I = I1 + I2 + I3
I1 = V / R1
I2 = V / R2
I3 = V / R3
If RT is the total resistance of the circuit then
I = V / RT
Therefore V / RT = V / R1 + V / R2 + V / R3
1 / RT = 1 / R1 + 1 / R2 + 1 / R3
If Req is the equivalent resistance of the circuit then it is calculated from adding the reciprocal values of individual resistances (1/R). The inverse of this algebraic sum will give the equivalent resistance. The equation for equivalent resistance Req is shown below for a parallel resistive circuit of n resistors.
(1/Req) = (1/R1) + (1/R2) + (1/R3) + ……… + (1/Rn)
An observation can be made from the above equation that the equivalent resistance of resistors connected in parallel is always smaller than the resistance of smallest resistor.
If there are two resistors in parallel then the equivalent resistance is
(1/Req) = (1/R1) + (1/R2)
REQ = R1 * R1 / (R1 + R2)
If two resistors of equal resistance R are connected in parallel combination then the equivalent resistance of the combination is R / 2.
Similarly, if three resistors of equal resistance R are connected in parallel combination then the equivalent resistance of the combination is R / 3.
The parallel connection of resistors gives the value of Conductance. Conductance is the reciprocal of resistance. It is generally represented by the symbol G. The units of Conductance are Siemens represented by the symbol S. Previously the units of conductance are Mho (℧) which is backward spelling of Ohm and the symbol is upside down representation of Ω.
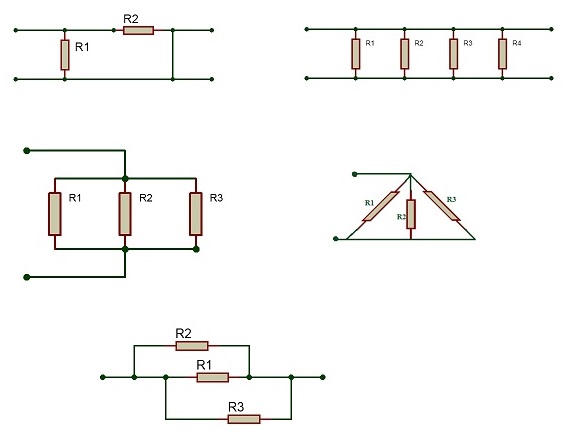
Even though the parallel resistors are connected between two nodes, the representation of this connection can take any of the following form.
All the above mentioned combinations are parallel resistive circuits and all the rules of parallel resistorsare applicable to above mentioned combinations too.
Current Calculation
Current in each branch of a parallel resistive circuit is different from the other. Since the voltage across each resistor is same, the current flowing through each resistor is dependent on the resistance of that resistor. Hence if the resistance value in a branch is different from the other branch then the current in those branches will be different. The value of that current can be determined by using Ohm’s Law.
Consider a parallel network of two resistors with supply voltage V between two points A and B.
Let I be the total current in the following circuit.
Let the current flowing through the resistor R1 be IR1 and the current flowing through the resistor R2 be IR2.
Then according to Kirchhoff’s Current Law, “the total current entering a circuit is equal to that leaving the circuit.”
If IT is the total current then
IT = IR1 + IR2
As the voltage drop across each resistor is same
IR1 = V / R1
And IR2 = V / R2
If a parallel resistive circuit consisting of n resistors is considered, then the total current in the circuit is
ITotal = IR1 + IR2 +…. + IRn
If the series resistive circuits are called Voltage Divider Circuits then similarly the parallel resistive circuits are called Current Divider Circuits.
If a parallel resistive circuit of n resistors with different resistances is considered then it is possible to have n different paths for the current to flow and n different values of current through that paths. The resistors in a parallel combination can be interchanged without affecting the total current and equivalent resistance.
Resistors in Parallel Example
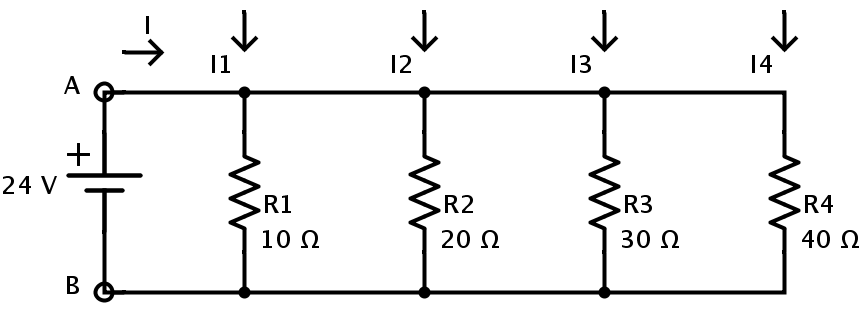
- Consider the following circuit where four resistors R1, R2, R3 and R4 are connected in parallel.
The resistance values of each resistor are
R1 = 10 Ω
R2 = 20 Ω
R3 = 30 Ω
R4 = 40 Ω
The supply voltage is V = 24V
The total current in the circuit can be calculated by two methods.
First method is to calculate individual currents flowing through each resistor.
If I1 is the current flowing through the resistor R1, then according to Ohm’s law
I1 = V / R1 = 24/10 = 2.4 A
Similarly if I2 is the current flowing through the resistor R2, thenaccording to Ohm’s law
I2 = V / R2 = 24/20 = 1.2 A
If I3 is the current flowing through the resistor R3, thenaccording to Ohm’s law
I3 = V / R3 = 24/30 = 0.8 A
And if I4 is the current flowing through the resistor R4, thenaccording to Ohm’s law
I4 = V / R4 = 24/40 = 0.6 A
If ITOTAL is the total current in the circuit, then according to Kirchhoff’s Current law,
ITOTAL = I1 + I2 + I3 + I4 = 2.4 + 1.2 + 0.8 + 0.6 = 5A
The second method to calculate current is by finding out the equivalent resistance of the circuit.
The equivalent resistance of the circuit is
1/REQ = (1/ R1) + (1/R2) + (1/ R3) + (1/R4)
1/REQ = (1/10) + (1/20) + (1/30) + (1/40)
REQ = 1/2.083 = 4.8 Ω
This single resistor can be used to replace all the resistors in the parallel combination.
∴ ITOTAL = V/REQ = 24/4.8 = 5A.
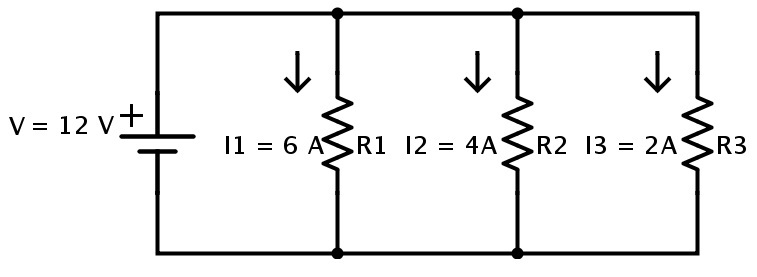
Consider the following circuit where three resistors R1, R2 and R3 are connected in a parallel combination.
The current flowing through R1 is I1 = 6A
The current flowing through R2 is I2 = 4A
The current flowing through R3 is I3 = 2A
In parallel resistive circuits, the voltage across each resistor is same and is equal to the supply voltage.
Here the supply voltage is V = 12 V.
If V1 is the voltage across the resistor R1, V2 is the voltage across the resistor R2 and V3 is the voltage across the resistor R3 then
V = V1 = V2 = V3 = 12V
Then according to Ohm’s law
R1 = V1 / I1
R1 = 12 / 6
R1 = 2 Ω
R2 = V2 / I2
R2 = 12 / 4
R2 = 3 Ω
R3 = V3 / I3
R3 = 12 / 2
R3 = 6 Ω
Applications
The concept of resistors in parallel is used in the analysis of Wheatstone bridge circuit. Resistors in parallel combination act as Current Divider Circuit. This current divider concept is use full in applications like Analog to Digital Converters and Digital to Analog Converters.


2 Responses
Really impressed the way you guys explained each and every topic very very clearly..Thank a Lot
Nice…. good job