For analysing the linear electric circuits that consists of two or more independent sources (Voltage or current or both), superposition theorem is extremely used (particularly for time domain circuits with elements operated at different frequencies). If a linear DC circuit has more than one independent source, we can find the current (through a resistance) and voltage (across the resistance) by using nodal or mesh analysis methods.
Alternatively , we can use the superposition theorem that adds each individual source effect on the value of the variable to be determined. This means superposition theorem considers the each source in a given circuit separately for finding the value of the variable (whether current or voltage) and finally produce the resultant variable by adding all the variables caused by each source effect. Even though it is of complex procedure, but still can be applied for any linear circuit.
Outline
ToggleSuperposition Theorem Statement
The superposition theorem states that in any linear bilateral network that consisting of two or more independent sources, current through (or voltage across) an element is the algebraic sum of the currents through (voltages across) that element caused by each independent source acting alone with all other sources are replaced by their internal resistances. We know that as long as the linearity exists between the source and contribution, the total contribution due to various sources acting simultaneously is equal to the algebraic sum of individual contributions due to individual source acting at a time.
Therefore, if the circuit consists of N independent sources, we have to analyse N circuits, each will produce a result with respect to each individual source. And finally these individual results must be added to get the whole analysis of the circuit. Therefore, this require more work however, this theorem will be very useful in analysing the various parts of a complex circuit.
Steps to Analyse Superposition Theorem
1. Consider the various independent sources in a given circuit.
2. Select and retain one of the independent sources and replace all other sources with their internal resistances or else replace the current sources with open circuits and voltage sources with short circuits.
3. To avoid confusion re-label the voltage and current notations suitably.
4. Find out the desired voltage/currents due to the one source acting alone using various circuit reduction techniques.
5. Repeat the steps 2 to 4 for each independent source in the given circuit.
6. Algebraically add all the voltages/currents that are obtained from each individual source (Consider the voltage signs and current directions while adding).
[adsense2]
Superposition Theorem Example :
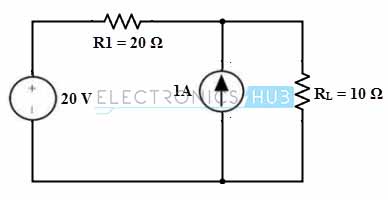
1. Let us consider the below simple DC circuit to apply the superposition theorem such that we will obtain the voltage across the resistance 10 Ohms (load terminals). Consider that in a given circuit there are two independent sources as voltage and current sources as shown in figure.
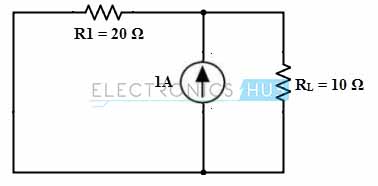
2. First, we retain one source at a time that means , only voltage source is acting in the circuit and the current source is replaced with internal resistance (infinite) so it becomes open circuited as shown in figure.
Consider VL1 is the voltage across the load terminals with voltage source acting alone, then
VL1 = Vs × RL / (RL + R1)
= 20 × 10 / (10 + 20)
= 6. 66 Volts
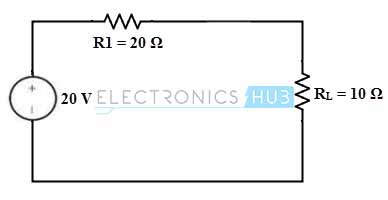
3. Retain the current source alone and replace the voltage source with its internal resistance (zero) so it becomes a short circuited as shown in figure.
Consider that VL2 is the voltage across the load terminals when current source acting alone. Then
VL2 = IL × RL
IL = I × R1 / (R1 + RL)
= 1 × 20 / (20 +30)
= 0.4 Amps
VL2 = 0.4 × 10
= 4 Volts
Therefore, according the superposition theorem, the voltage across the load is the sum of VL1 and VL2
VL = VL1 + VL2
= 6.66 + 4
= 10.66 Volts
Example 2:
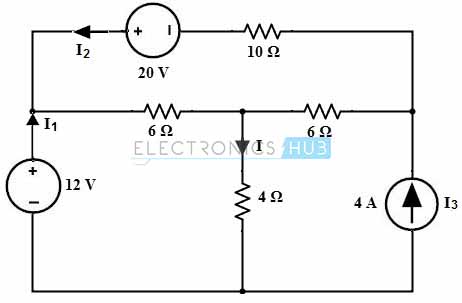
Consider the below circuit to which we are going to determine the current I through the 4 ohm resistor using superposition theorem.
Consider I1, I2 and I3 are the currents due to sources 12v, 20V and 4A sources respectively. Then, based superposition theorem I = I1 + I2 + I3. So let’s determine these currents with each individual source.
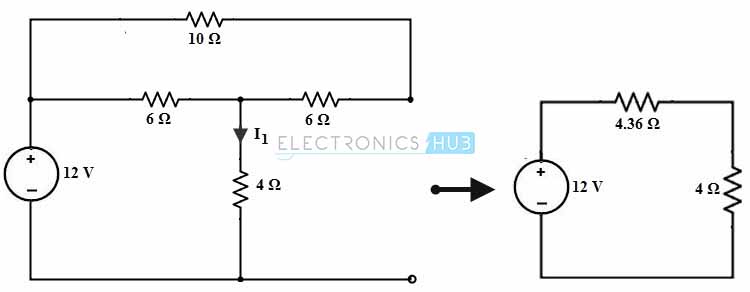
Only with 12V Voltage source:
Consider the below circuit where only 12V source is retained in the circuit and other sources are replaced by their internal resistances.
By combining the resistance 6 ohm with 10 ohm we get 16 ohm resistance which is parallel with 6 ohm resistance. Then this combination produce, 16 × 6 / (16 + 6) = 4.36 ohm. Therefore the equivalent circuit will be as shown in figure.
Then the current through 4 ohms resistance,
I1 = 12 / 8.36
= 1.43 A
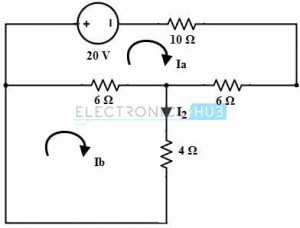
Only with 20 V Voltage Source:
Retain only 20 V voltage source and replace other sources with their internal resistance, then the circuit becomes as shown below.
Apply the mesh analysis to the loop a, we get
22Ia – 6Ib + 20 = 0
22Ia – 6Ib = -20 ……………….(1)
For Loop b, we get
10Ib – 6Ia = 0
Ia = 10Ib/6
Substituting Ib in equation 1
22 (10Ib/6) – 6Ib = -20
Ib = – 0.65
Therefore, I2 = Ib = -0.65
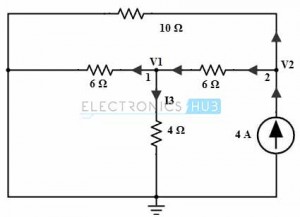
Only with 4A Current Source
Consider the below circuit where only current source is retained and other sources are replaced with their internal resistances.
By applying nodal analysis at node 2 we get,
4 = (V2/10) + (V2 – V1)/6 ………………..(2)
At node1,
(V1/6) + (V1/4) = (V2 – V1)/ 6
V2 = 3.496 V1
Substituting V2 in equation 2, we get
V1 = 0.766 Volts.
Therefore I3 = V1/4
= 0.766/4
= 0.19 Amps.
Thus, as per the superposition theorem, I = I1 + I2 + I3
= 1.43 – 0.65 + 0.19
= 0.97 Amps.
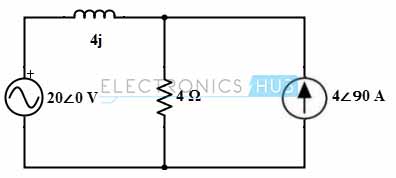
Superposition Example Using AC Circuit:
Consider the below AC circuit, to which we are going to determine the value of current in the 4 ohm resistor using superposition theorem.
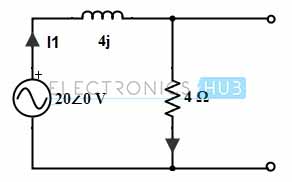
Case 1: Only with 20∠0 Voltage Source
By retaining the voltage source alone in the circuit, the current flow through the circuit is determined as
I1 = 20∠0/ (4 + j4)
= 20∠0 / (5.65∠45)
= 3.53∠- 45 or 2.49 –j2.49 A
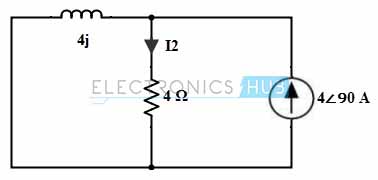
Case 2: Only with 4∠90 Current Source
By retaining the current source alone in the circuit, the current I2 through the circuit is determined as
By current division method, I2 = 4∠90 × 4j/ (4 + j4)
= 4∠90 × 4∠90 (5.65∠45)
= 4∠90 × 0.707∠45
= 2.828∠135 or -1.99 + j1.99 A
The resultant current through the resistor 4 ohms is I = I1 + I2
= 3.53∠- 45 + 2.828∠135
= 0.785∠45 or 0.56 + j0.56 A
Limitations of Superposition Theorem
1. For power calculations superposition theorem cannot be used as this theorem works based on the linearity. Because the power equation is not linear as it is the product of voltage and current or square of the current or square of the voltage. Thus the power consumed by the element in a given circuit with superposition theorem is not possible.
2. If the choice of the load is variable or the load resistance changes frequently, then it is required to perform every source contribution of current or voltage and their sum for every change in load resistance. So this very complex procedure for analysing complex circuits.
3. This theorem applicable for only linear circuits and for non linear circuits (Having transistors and diodes) we can not apply.
4. This theorem is applicable only if the circuit has more than one source.


2 Responses
Good explaination
Good explanation