In this tutorial, we will learn about Kirchhoff’s Laws. Kirchhoff’s Current Law or KCL and Kirchhoff’s Voltage Law or KVL are two very important mathematical equalities in electrical circuit analysis.
Outline
ToggleIntroduction
Many of the electrical circuits are complex in nature and the computations required to find the unknown quantities in such circuits, using simple ohm’s law and series/parallel combination simplifying methods is not possible. Therefore, in order to simplify these circuits Kirchhoff’s laws are used.
These laws are the fundamental analytical tools that are used to find the solutions of voltages and currents in an electric circuit whether it can be AC or DC. Elements in an electric circuit are connected in numerous possible ways, thus to find the parameters in an electrical circuit these laws are very helpful.
Before going to know more about Kirchhoff’s law, we have to consider some of the terms related to electric circuits.
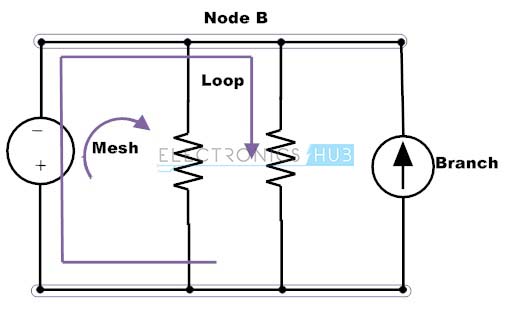
Node: Node or junction is a point in the circuit where two or more electrical elements are connected. This specifies a voltage level with a reference node in a circuit.
Branch: The continuous conducting path between two junctions which contains electrical element in a circuit is referred as branch.
Loop: In an electrical circuit a loop is an independent closed path in a circuit that follows the sequence of branches in such a way that it must start and ends with same node and it shouldn’t touch any other junction or node more than once.
Mesh: In an electrical circuit mesh is a loop that doesn’t contain any other loop in its interior.
Kirchhoff’s Laws
In 1847, Gustav Robert Kirchhoff, a German physicist was developed these laws to describe the voltage and current relationship in an electric circuit. These laws are: Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL).
Kirchhoff’s Current Law (KCL)
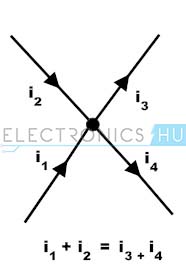
This is also called as the law of conservation of charge because charge or current cannot be created or destroyed at the junction or node. It states that the algebraic sum of currents at any node is zero. Thus the current entering at a node must be equal to sum of current out of the node.
In the above figure, currents I1 and I2 are entering to the node while the currents I3 and I4 are leaving from the node. By applying KCL at the node , assume that entering currents are positive and leaving currents are negative ,we can write as
I1 + I2 + (-I3) + (-I4) = 0
I1 + I2 = I3 + I4
Example Problem of KCL
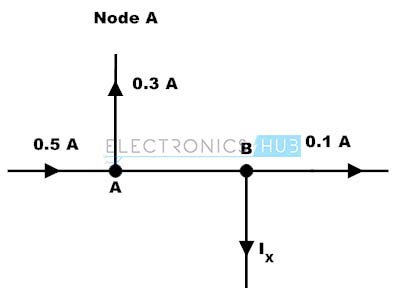
Consider the below figure where we have to determine the currents IAB and Ix by using KCL .
By applying Kirchhoff’s Current Law at point A, we get
IAB = 0.5 – 0.3
IAB = 0.2 Amps
Similarly by applying KCL at point B, we get
IAB = 0.1 + Ix
0.2 = 0.1 + Ix
Ix = 0.2 – 0.1 = 0.1 Amps
Kirchhoff’s Voltage Law (KVL)
Kirchhoff’s Voltage Law states that the algebraic sum of voltages in a closed path is equal to zero that is the sum of source voltages is equal to the sum of voltage drops in a circuit. If the current flows from higher potential to lower in an element, then we consider it as a voltage drop.
If the current flows from lower potential to higher potential, then we consider it as a voltage rise. Thus, the energy dissipated by the current must be equal to the energy given by the power supply in an electric circuit.
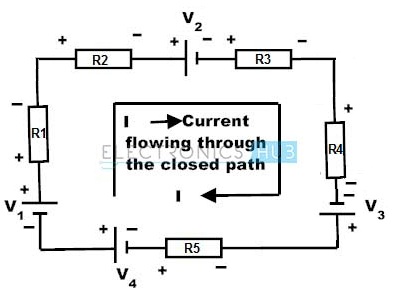
Consider above circuit where the direction of current flow is taken clockwise. Various voltage drops in the above circuit are V1 is positive, IR1is negative (drop in voltage), IR2 is negative (drop in voltage), V2 is negative, IR3 is negative (drop in voltage), IR4 is negative (drop in voltage), V3 is positive, IR5 is negative and V4 is negative. By applying KVL, we get
V1 + (-IR1) + (-IR2) + (-V2) + (-IR3) + (-IR4) + V3 + (-IR5) + (-V4) = 0
V1 – IR1 – IR2 – V2 – IR3 – IR4 + V3 – IR5 – V4 = 0
V1 – V2 + V3 – V4 = IR1+ IR2 +IR3 + IR4 + IR5
Hence the KVL is also known as the law of conservation of electrical energy because the sum of voltage drops (product of resistance and current) is equal to the sum of voltage sources in a closed path.
Kirchhoff’s Voltage Law Example
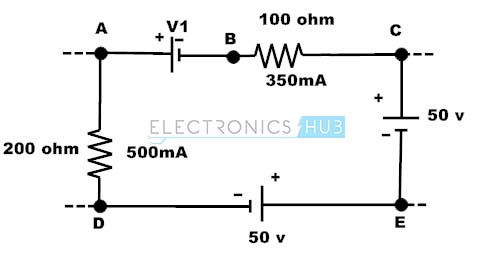
1. Let us consider the single loop circuit which is shown below and assume the current flow direction as DEABCD closed path. In this circuit, by using KVL we have to find the voltage V1.
By applying KVL to this closed loop, we can write as
VED + VAE + VBA + VCB + VDC = 0
Where
Voltage of point E with respect to point D, VED = -50 V
Voltage of point D with respect to point C, VDC = -50 V
Voltage of point A with respect to point E. VAE = I * R
VAE = 500m* 200
VAE = 100 V
Similarly Voltage at point C with respect to pint B, VCB = 350m*100
VCB = 35V
Consider voltage at point A with respect to point B, VAB = V1
VBA= -V1
Then by using KVL
-50 + 100 – V1 + 35 – 50 = 0
V1 = 35 Volts
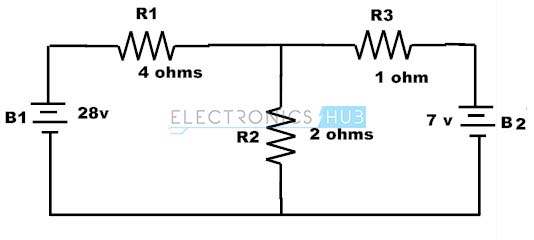
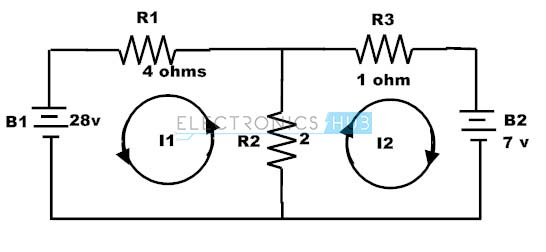
2. Consider the below typical two loop circuit where we have to find the currents I1 and I2 by applying the Kirchhoff’s laws.
There are two loops inside the circuit and consider the loop paths as shown in figure.
By applying KVL to these loops we get
For first loop,
2 (I1 + I2) + 4I1 – 28 = 0
6I1 + 2I2 = 28 ——— (1)
For second loop,
-2(I1 + I2) – 1I2 + 7 = 0
-2I1 – 3I2 = -7 ——– (2)
By solving the above 1 and 2 equations we get,
I1 = 5A and I2 = -1 A
Example Problem on Kirchhoff’s laws
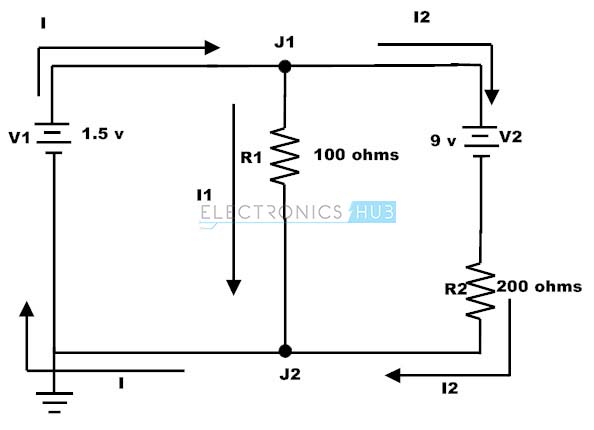
Now let us use both Kirchhoff’s current and voltage laws to find the current and voltage drops in below circuit. Similar to the above problem this circuit also contains two loops and two junctions. Consider the current direction given in the figure.
Apply Kirchhoff’s current law at both junctions, then we get
At junction 1, I = I1 + I2
At junction 2, I1 + I2 = I
Apply Kirchhoff’s voltage law to the both loops, then we get
In first loop,
1.5 V – 100 I1 = 0
I1 = 1.5 / 100
= 0.015 Amps
In second loop
100(I1- I2) – 9V – 200I2 = 0
100I1- 300I2 = 9
Substituting I1 value in the above equation then
1.5 – 300I2 = 9
– 300I2 = 7.5
I2 = -0.025
Then the current at the junction I = I1 + I2
I = 0.015 – 0.025
I = – 0.01
Applications of Kirchhoff’s Laws
- By using these laws, we can find the unknown resistances, voltages and currents (direction as well as value).
- In the branch method, finding the currents through each branch carried by applying KCL at every junction and KVL in every loop of a circuit.
- In the loop current method, finding current through each independent loop is carried by applying KVL for each loop and counting all the currents in any element of a circuit.
- Used in nodal method of finding voltages and currents.
- These laws can be applied to analyse any circuit regardless of the composition and structure of it.


4 Responses
I want conversion of A(B+C)(C’+D’)
IT IS VERY USEFUL ARTICLE
It is very useful, for beginners.
It,s very helpful for me actually it’s a good introduction of kirchhoff’s law and again very very thanks to you 😀