We use the Electrical Energy provided by our utility company to provide us with light, heat, running appliances etc. Since electric potential (voltage) and current are the two quantities available to us when the utility supplies electrical energy, these two are the main parameters that determine the Electric Power. In this guide, let us take a close look at Electric Power, the electric power formula in AC and DC Circuits.
Outline
ToggleWhat is Electric Power?
Electrical Energy is one of the widely used forms of energy in our day to day lives whether it is in the form of AC Mains power or batteries. Our utility company supplies this electrical energy in the form of electric potential and current and the rate at which electrical energy transfers in an electrical circuit is known as Electrical Power.
In terms of Physics, Energy is the ability to do Work and the rate of doing that Work is known as Power.
So, if P is the Power, W is the Work and t is the time, then
Power P = Work done in unit time = W/t
The units of power are Watts.
We know that the Electric Potential is the amount of Work done in moving a unit charge and current is the rate of movement of charge.
Using the above statement, we can rewrite the previous power equation as:
P = W/t = (W/Q) × (Q/t) Watts
The first term (W/Q) represents the electric potential (V) while the second term (Q/t) represents the current (I).
So, Electric Power P = V × I.
Electric Power Formula in AC & DC Circuits
Depending on the type of current in the circuit i.e., Alternating Current or Direct Current, the Electric Power can be further classified into AC Power and DC Power.
Let us now see different electric power formulas in both DC and AC Circuits.
Power Formulas in DC Circuits
In simple DC Circuits i.e., electric circuits with DC power supply, the power formula is given below:
P = V × I
Power in resistive DC Circuits is just the product of voltage and current.
We can derive further Power formulas by applying Ohm’s Law. According to Ohm’s Law, the voltage in a circuit (or component) is a product of the resistance and the current.
V = I × R
So, if we use this equation in the above Power Formula, we get
P = V × (V/R) = V2/R
P = (I×R) × I = I2R
Depending on the available quantities, you can use one of the three power formulas for calculating DC Power.
Power Formulas in AC Circuits
Measuring power in DC Circuits is very simple as all you have to do multiply the voltage and current. But the same is not possible in AC Circuits as the values of voltage and current are continuously changing both in terms of magnitude and direction (sign).
The values of alternating voltage and current are usually written as
VAC = VP × sin(ωt) and IAC = IP × sin(ωt)
To calculate AC Power, we have to somehow calculate the average values of voltage and current. Mathematically, we use Root Mean Square or RMS to determine the average values of sinusoidal functions.
If VRMS is the RMS Value of the AC Voltage and IRMS is the RMS value of the AC Current, then the Average AC Power is
PAC (Average) = VRMS × IRMS
If f(t) is a function of time t, then its RMS value is
Applying the above formula to our alternating voltage and current sinusoidal values, we get:
VRMS = VP /√2 and IRMS = IP /√2
The power we calculated earlier (PAC (Average)) is actually known as Apparent Power. It is nothing but the product of average (or effective) voltage and current i.e., its is the maximum average power delivered to a purely resistive load.
But inductors and capacitors have phase shifts and reactance. So, with inductors and capacitors, there are two more ways to define power in AC Circuits. They are Real Power (Active Power) and Reactive Power.
Real Power is also known as Active Power and is the power dissipated in the circuit due to its resistive elements.
Active Power = VRMS × IRMS × cos(θ), where θ is the phase angle by which the voltage leads current.
Reactive Power is the power dissipated in the circuit due to inductance and capacitance (or reactance).
It is given as Reactive Power = VRMS × IRMS × sin(θ)
So, we can say that (apparent power)2 = (real power)2 + (reactive power)2
DC and AC Power Formulas
The following table lists out all the power formulas for both AC and DC circuits.
| Circuit | Power |
| DC | P = V × I |
| P = V2/R | |
| P = I2 × R | |
| Single Phase AC Real Power | ½ VP × IP × cos(θ) = VRMS × IRMS × cos(θ) |
| Single Phase AC Reactive Power | ½ VP × IP × sin(θ) = VRMS × IRMS × sin(θ) |
| Three Phase AC Real Power | 3 × VL-N × IL-N × cos(θ) = √3 × VL-L × IL-L × cos(θ) |
| Three Phase AC Reactive Power | 3 × VL-N × IL-N × sin(θ) = √3 × VL-L × IL-L × sin(θ) |
Conclusion
A simple guide on understanding Electric Power. We learned what is electric power, how to calculate power in DC and AC Circuits using respective power formulas, real, reactive and apparent power in AC Circuits and also power formula for both single phase and three phase AC circuits.

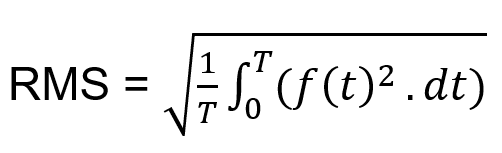

One Response
Hi gentleman friends i just see your webpages really amazing….it is a very useful to life on hand instantly…. iam very thankful today your Team.. I am just +2pass person…
By
MkumaR
Tamilnadu
Country code(+91)💐🎂👍