In this tutorial, we will learn about two of the basic and important concepts of Physics. They are Electric Potential and Electric Potential Difference also known as Voltage.
If you are looking for some basics of electricity like from the concepts of static electricity, then refer to the tutorial on ELECTRICITY BASICS.
Outline
ToggleIntroduction
In the previous tutorials on Electric Charge, Coulomb’s Law and Electricity, we barely discussed about the concept of Electric Potential and Electric Potential Difference. Electricity can be described using two terms known as Energy and Voltage.
From the previous discussion on Coulomb’s Law, we are familiar that a force acing on an object will result in a mechanical work i.e. in case of electric charge, electric force can do work on electric charges (or charged objects).
Analogous to gravitation energy, the Electrical Work is related to Electric Potential Energy. Using this electric potential energy, we can define a special quantity known as Electric Potential.
Electric Potential Energy
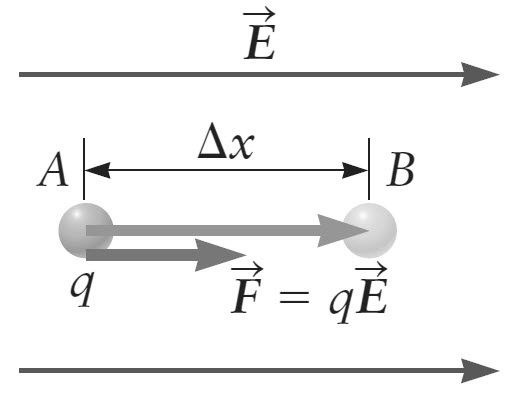
Before going into the concepts of Electric Potential and Electric Potential Difference, let us review the relation between force and work. The following image shows a region of space where the electric field E is constant i.e. it has same magnitude and direction at all points.
A point charge q in this region experiences an electric force given by the following equation:
F = qE
Let us assume that the charge is moved from point A to point B which are at a distance ∆x and for the sake of simplicity, let the direction of this displacement be parallel to the electric force F.
Now, according to the definition of work, it is equal to the product of force and the displacement. Therefore, the work done by the electric force F on the charge q is given by
W = F ∆x
The nature of electric force is conservative i.e. irrespective of the path between A and B, the work done on the charge q will be the same. Now with all this information, we are ready to define the Electric Potential Energy represented by PEELE.
For a conservative force (like the electric force here), if W is the work done by the force, then the change in potential energy is equal to -W. Hence, if an electric force does W amount of work on a charged particle, then the change in the Electric Potential Energy is:
∆ PEELE = -W
From all the earlier mentioned equations, the change in electric potential energy when a charged object is moved from point A to B in a constant electric field region is
∆ PEELE = -W = -F ∆x = -qE ∆x
Electric Potential
The Electric Potential Energy discussed in the previous section is not a property of a single charge but rather it is a property of a point charge in an electric field or a system of charges. If we take two point charges into consideration, then the potential energy is associated with Coulomb’s forces that act between them.
Hence, potential energy of two point charges q1 and q2 depends on both the charges and is given by the following equation:
PEELE = k.q1.q2 / r
Keeping this in mind, let us take a different view of electric potential energy as a property associated with only electric field.
For a test charge q, we can measure the electric field by measuring the force on the test charge.
The following equation will give the relation between electric force and electric field.
F = qE
From this, the electric field can be deduced as:
E = F / q
Focusing on the electric field, if this field is due to a point charge Q, then the magnitude of electric field is:
E = k.Q / r2
From the above equation we can say that the electric field doesn’t depend on the test charge q. treating electric potential energy in a similar manner, we can measure the potential energy of a charge q placed at a particular location.
The Electric Potential V can then be defined using the following equation:
V = PEELE / q
Electric Potential V is defined as the potential energy per unit charge.
Formula of Electric Potential
The electric potential energy between two Charges Q and q is given by
PEELE = k.Q.q / r
From the above definition of electric potential, V = PEELE / q
Therefore, V = k.Q / r
Where k is the Coulomb’s Constant.
Based on the above equation, we can conclude that electric potential is directly proportional to the charge Q while it is inversely proportional to the distance r.
Units of Electric Potential
The electric potential is often referred to as the potential. In the honour of Alessandro Volta, the SI unit of potential is termed as Volt (V).
We know that electric potential is electric potential energy over the charge. Therefore, volt can be related to other SI units as follows:
Units of Electric Potential: 1 V = 1 J/C = 1 N . m/C
Electric Potential Difference (Voltage)
The next important topic of discussion is Electric Potential Difference also known as Voltage. The definition of voltage is something like this: When a work is done on a charge to move it from position A to B i.e. its potential energy is changed, electric potential difference or voltage is the difference between the initial electric potential and final electric potential.
It is often represented as ∆V and if VA is the electric potential at point A and VB is the electric potential at point B, then
∆V = VA – VB
The term Voltage is a common name for Electric Potential Difference and whenever the term voltage is used, it usually means the potential difference between two points. For example, when we talk about voltage of a battery, we usually mean the potential difference between the two terminals of the battery.
Also, voltage and energy are not the same. Voltage is energy per unit charge. Hence, a 12V Motorcycle battery and a 12V Car battery can store different energies.
Example
Consider a 12V Motorcycle battery that can move 4000 C of charge while a 12V Car battery can move a whooping 50000 C of charge.
Now we can calculate the energy delivered by each battery as follows:
We know that potential V = Potential Energy / Charge. Therefore, Energy can be calculated as Energy = Potential X Charge.
Energy Delivered by Motorcycle Battery = 12V X 4000C = 48 x 103 J
Energy Delivered by Car Battery = 12V X 50000C = 60 x 104 J
Exercise
Perform a small calculation and find out how much energy does a 1.5V AA battery have if it can move 100 C of charge.