In electronics, an Amplifier is a circuit which accepts an input signal and produces an undistorted large version of the signal as its output. In this tutorial, we will learn about an important configuration of an Op Amp called the Non-Inverting Amplifier. In Non Inverting Operational Amplifiers, the input is fed to the non-inverting terminal and the output is in phase with the input.
Outline
Toggle- Operational Amplifiers
- Ideal Non-Inverting Amplifier Circuit
- Voltage Gain of Non-Inverting Operational Amplifier
- Virtual Short
- Input Impedance of Non-Inverting Amplifier
- Output Impedance of Non-Inverting Amplifier
- Voltage Follower Circuit
- Non-Inverting Amplifier Example
- Non-Inverting Amplifier Summary
- Conclusion
Operational Amplifiers
An Operational Amplifier or more commonly known as Op Amp is essentially a multi stage high gain differential amplifier which can be used in several ways. Two important circuits of a typical Op Amp are:
- Inverting Amplifier
- Non-Inverting Amplifier
A non-inverting amplifier is an op-amp circuit configuration that produces an amplified output signal and this output signal of the non-inverting op-amp is in-phase with the applied input signal.
In other words, a non-inverting amplifier behaves like a voltage follower circuit. A non-inverting amplifier also uses a negative feedback connection, but instead of feeding the entire output signal to the input, only a part of the output signal voltage is fed back as input to the inverting input terminal of the op-amp.
The high input impedance and low output impedance of the non-inverting amplifier make the circuit ideal for impedance buffering applications.
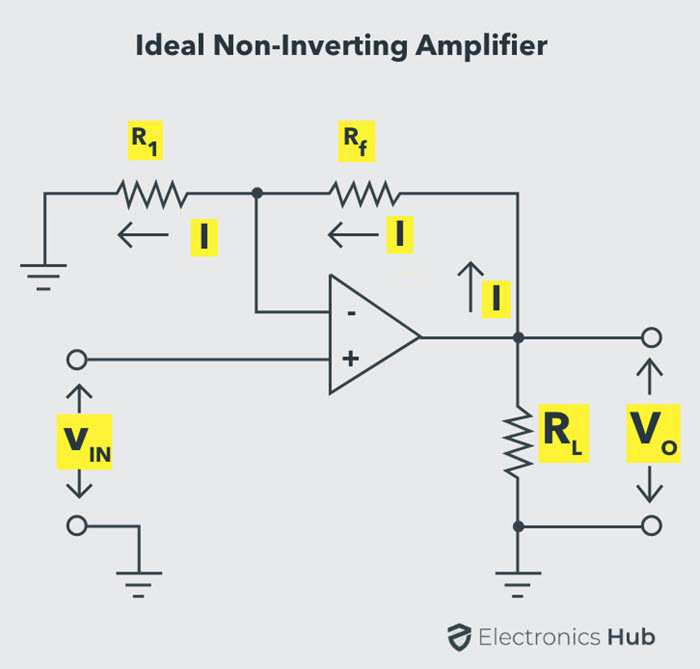
Ideal Non-Inverting Amplifier Circuit
The circuit diagram of an ideal non-inverting amplifier is as shown in the figure below.
From the circuit, it can be seen that the R2 (Rf in the above picture) and R1 (R1 in the above picture) act as a potential divider for the output voltage and the voltage across resistor R1 is applied to the inverting input.
When the non-inverting input is connected to the ground, i.e., VIN = 0, the voltage at the inverting input terminal must also be at ground level; if not, any voltage difference between the input terminals would be amplified to move the inverting input terminal back to the ground level (inputs of the Op Amp will always be at the same voltage).
Since the inverting input terminal is at ground level, the junction of the resistors R1 and R2 must also be at ground level. This implies that the voltage drop across R1 will be zero. As a result, the current flowing through R1 and R2 must be zero. Thus, there are zero voltage drops across R2, and therefore the output voltage is equal to the input voltage, which is 0V.
When a positive-going input signal is applied to the non-inverting input terminal, the output voltage will shift to keep the inverting input terminal equal to that of the input voltage applied. Hence, there will be a feedback voltage developed across resistor R1,
VR1 = VIN = VOUT R1 / (R1 + R2)
Voltage Gain of Non-Inverting Operational Amplifier
From the above equation, of VIN in terms of VOUT, the closed-loop voltage gain of the non-inverting amplifier ACL can be calculated as:
ACL = VOUT / VIN
= (R1 + R2) / R1
ACL = 1 + (R2 / R1)
or ACL = 1 + (Rf / R1)
The above gain equation is positive, indicating that the output will be in-phase with the applied input signal. The closed-loop voltage gain of a non-inverting amplifier is determined by the ratio of the resistors R1 and R2 used in the circuit.
Practically, non-inverting amplifiers will have a resistor in series with the input voltage source, to keep the input current the same at both input terminals.
Virtual Short
In a non-inverting amplifier, there exists a virtual short between the two input terminals. A virtual short is a short circuit for voltage, but an open-circuit for current. The virtual short uses two properties of an ideal op-amp:
- Since RIN is infinite, the input current at both the terminals is zero.
- Since Open Loop Gain AOL is infinite, the difference voltage (V1 – V2) is always zero.
Although virtual short is an ideal approximation, it gives accurate values when used with heavy negative feedback. As long as the op-amp is operating in the linear region (not saturated, positively or negatively), the open-loop voltage gain approaches infinity and a virtual short exists between two input terminals.
Because of the virtual short, the inverting input voltage follows the non-inverting input voltage. If the non-inverting input voltage increases or decreases, the inverting input voltage immediately increases or decreases to the same value. This action is often referred to as “Bootstrapping”.
Input Impedance of Non-Inverting Amplifier
The input impedance of an operational amplifier circuit is given as:
ZIN = (1 + AOL β) Zi
Where, AOL is the open-loop gain of op-amp
Zi is the input impedance of op-amp without any feedback
β is the feedback factor
For a non-inverting amplifier, the feedback factor is given as:
β = R2 / (R1 + R2)
β = 1 / ACL
Therefore, for a non-inverting amplifier circuit, the input impedance is given by the equation,
ZIN = {1 + (AOL / ACL)} Zi
Output Impedance of Non-Inverting Amplifier
The output impedance of an op-amp is expressed as:
ZOUT = Z0 / (1+ AOL β)
Since, β = 1 / ACL for a non-inverting amplifier, the impedance is given as,
ZOUT = Z0 / {1 + (AOL / ACL)}
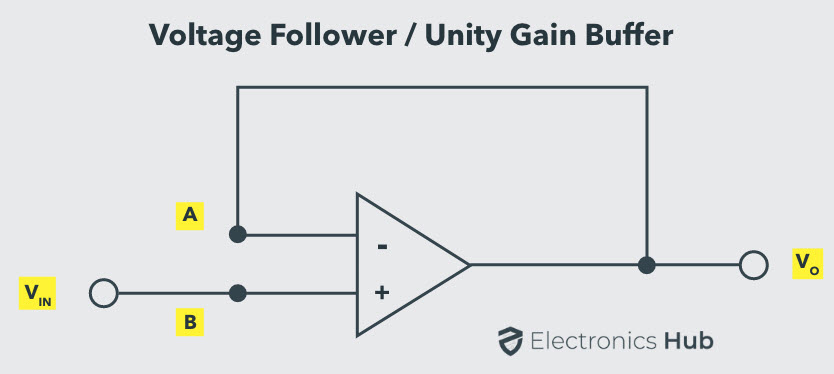
Voltage Follower Circuit
Voltage follower is one of the simplest uses of an operational amplifier, where the output voltage is exactly same as the input voltage applied to the circuit. In other words, the gain of a voltage follower circuit is unity.
The output of the op-amp is directly connected to the inverting input terminal, and the input voltage is applied at the non-inverting input terminal. The voltage follower, like a non-inverting amplifier, has very high input impedance and very low output impedance. The circuit diagram of a voltage follower is shown in the figure below.
It can be seen that the above configuration is the same as the non-inverting amplifier circuit, with the exception that there are no resistors used. The gain of a non-inverting amplifier is given as,
ACL = 1 + (R2 / R1)
In the voltage follower, the resistor R2 is equal to zero and R1 is infinite. So, the gain of the voltage follower will be equal to 1. Hence, a Voltage Follower is also commonly known as a Unity Gain Buffer.
The voltage follower or unity gain buffer circuit is commonly used to isolate different circuits, i.e., to separate one stage of the circuit from another and also used in impedance matching applications.
In practice, the output voltage of a voltage follower will not be exactly equal to the input voltage applied and there will be a slight difference. This difference is due to the high internal voltage gain of the op-amp.
NOTE: The open-loop voltage gain of an op-amp is infinite and the closed-loop voltage gain of the voltage follower is unity. This implies that by carefully selecting feedback components, we can accurately control the gain of a non-inverting amplifier.
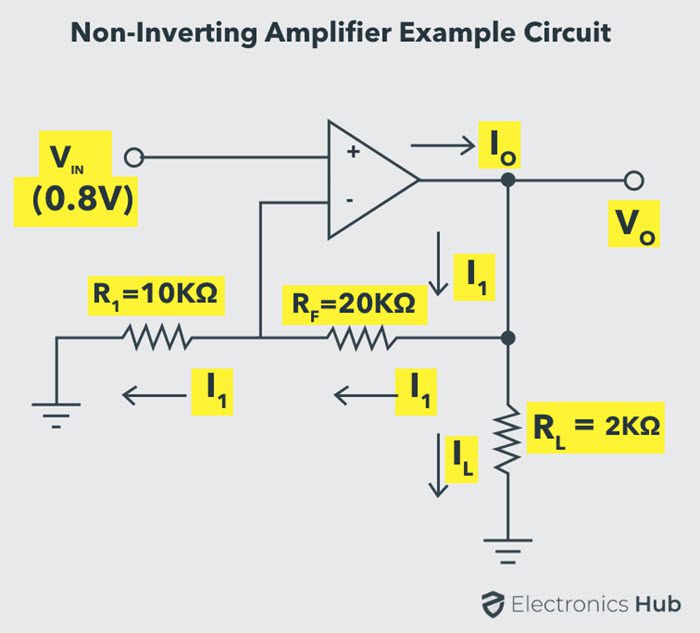
Non-Inverting Amplifier Example
For the non-inverting amplifier shown in the figure below, calculate the following:
i) The gain of the amplifier, ACL
ii) The output voltage, VO
iii) The current through the load resistor, IL.
iv) The output current, IO.
NOTE: Node A is at the non-inverting terminal of the Op-Amp and node B is at the inverting terminal (which is also the voltage divider point). These nodes are not shown in the above image.
Answer) The potential at node B is VIN and because of the virtual short,
VA = VB = VIN = 0.8 V
The current I1 is given as,
I1 = VA / R1 = 0.8V / 10 KΩ
I1 = 80 µA
Since the op-amp input current is zero, the same I1 must flow through the resistor Rf.
i) The gain of the non-inverting amplifier,
ACL = 1 + (Rf / R1) = 1 + (20 KΩ / 10 KΩ)
ACL = 3
ii) The output voltage,
VO = ACL * VIN = 3 * 0.8V
VO = 2.4 V
iii) Current through the load resistor,
IL = VO / RL = 2.4 / (2 * 103 Ω)
IL = 1.2 mA
iv) The output current,
From Kirchhoff’s Current Law (KCL), IO = I1 + IL
IO = 80 µA + 1.2 mA
IO = 1.28 mA
Non-Inverting Amplifier Summary
- A non-inverting amplifier uses a voltage-divider-bias negative feedback connection.
- The voltage gain is always greater than one.
- The voltage gain is positive, indicating that for AC input, the output is in-phase with the input signal and for DC input, the output polarity is the same as the input polarity.
- The voltage gain of the non-inverting op-amp depends only on the resistor values and is independent of the open-loop gain of the op-amp.
- The desired voltage gain can be obtained by choosing the appropriate values of the resistors.
Conclusion
A simple tutorial on Non Inverting Operational Amplifiers. You learned the circuit of an ideal non-inverting amplifier, voltage gain, input and output impedance, voltage follower application and an example circuit with all the important calculations.


6 Responses
i want to know more about band pass filter & all pass filter????
It is indeed a good idea to show a numerica example for my students who will see this site and try themselves on problems.
I think that the Gain of the Non-Inverting Operational Amplifier is A=1+R2/R1 , SINCE Vin is actually Vin=I*R1 and not I*R2.
Yes you are right! It’s a mistake in the article, but other than that it’s very informative
Corrected.
Thank you for the ‘feedback’.
yes