Error Correction and Detection Codes

In this tutorial, we will learn about some of the commonly used Error Correction and Detection Codes. We will see about error in digital communication, what are the different types of errors, some error correction and detection codes like Parity, CRC, Hamming Code, etc.

Introdcution

In digital systems, the analog signals will change into digital sequence (in the form of bits). This sequence of bits is called as “Data stream”. The change in position of single bit also leads to catastrophic (major) error in data output. Almost in all electronic devices, we find errors and we use error detection and correction techniques to get the exact or approximate output.

What is an Error

The data can be corrupted during transmission (from source to receiver). It may be affected by external noise or some other physical imperfections. In this case, the input data is not same as the received output data. This mismatched data is called “Error”.

The data errors will cause loss of important / secured data. Even one bit of change in data may affect the whole system’s performance. Generally the data transfer in digital systems will be in the form of ‘Bit – transfer’. In this case, the data error is likely to be changed in positions of 0 and 1 .

Back to top

Types Of Errors

In a data sequence, if 1 is changed to zero or 0 is changed to 1, it is called “Bit error”.

There are generally 3 types of errors occur in data transmission from transmitter to receiver. They are

• Single bit errors

• Multiple bit errors

• Burst errors

Single Bit Data Errors

The change in one bit in the whole data sequence , is called “Single bit error”. Occurrence of single bit error is very rare in serial communication system. This type of error occurs only in parallel communication system, as data is transferred bit wise in single line, there is chance that single line to be noisy.

Multiple Bit Data Errors

If there is change in two or more bits of data sequence of transmitter to receiver, it is called “Multiple bit error”. This type of error occurs in both serial type and parallel type data communication networks.

Burst Errors

The change of set of bits in data sequence is called “Burst error”. The burst error is calculated in from the first bit change to last bit change.

Here we identify the error form fourth bit to 6th bit. The numbers between 4th and 6th bits are also considered as error. These set of bits are called “Burst error”. These burst bits changes from transmitter to receiver, which may cause a major error in data sequence. This type of errors occurs in serial communication and they are difficult to solve.

Back to top

Error Detecting Codes

In digital communication system errors are transferred from one communication system to another, along with the data. If these errors are not detected and corrected, data will be lost . For effective communication, data should be transferred with high accuracy .This can be achieved by first detecting the errors and then correcting them.

Error detection is the process of detecting the errors that are present in the data transmitted from transmitter to receiver, in a communication system. We use some redundancy codes to detect these errors, by adding to the data while it is transmitted from source (transmitter). These codes are called “Error detecting codes”.

Types of Error detection

1. Parity Checking
2. Cyclic Redundancy Check (CRC)
3.  Longitudinal Redundancy Check (LRC)
4. Check Sum

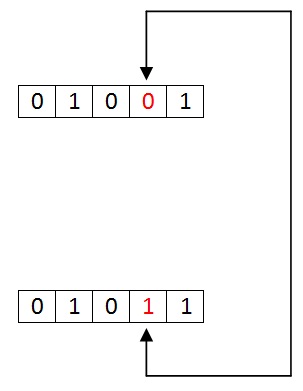
 Parity Checking

Parity bit means nothing but an additional bit added to the data at the transmitter before transmitting the data. Before adding the parity bit, number of 1’s or zeros is calculated in the data. Based on this calculation of data an extra bit is added to the actual information / data. The addition of parity bit to the data will result in the change of data string size.

This means if we have an 8 bit data, then after adding a parity bit to the data binary string it will become a 9 bit binary data string.

Parity check is also called as “Vertical Redundancy Check (VRC)”.

There is two types of parity bits in error detection, they are

• Even parity
• Odd parity

Even Parity

• If the data has even number of 1’s, the parity bit is 0. Ex: data is 10000001 -> parity bit 0
• Odd number of 1’s, the parity bit is 1. Ex: data is 10010001 -> parity bit 1

Odd Parity

• If the data has odd number of 1’s, the parity bit is 0. Ex: data is 10011101 -> parity bit 0
• Even number of 1’s, the parity bit is 1. Ex: data is 10010101 -> parity bit 1

NOTE: The counting of data bits will include the parity bit also.

The circuit which adds a parity bit to the data at transmitter is called “Parity generator”. The parity bits are transmitted and they are checked at the receiver. If the parity bits sent at the transmitter and the parity bits received at receiver are not equal then an error is detected. The circuit which checks the parity at receiver is called “Parity checker”.

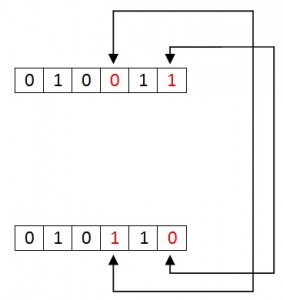
Messages with even parity and odd parity

Back to top

 Cyclic  Redundancy Check (CRC)

A cyclic code is a linear (n, k) block code with the property that every cyclic shift of a codeword results in another code word. Here k indicates the length of the message at transmitter (the number of information bits). n is the total length of the message after adding check bits. (actual data and the check bits). n, k is the number of check bits.
The codes used for cyclic redundancy check there by error detection are known as CRC codes (Cyclic redundancy check codes).Cyclic redundancy-check codes are shortened cyclic codes. These types of codes are used for error detection and encoding. They are easily implemented using shift-registers with feedback connections. That is why they are widely used for error detection on digital communication. CRC codes will provide effective and high level of protection.

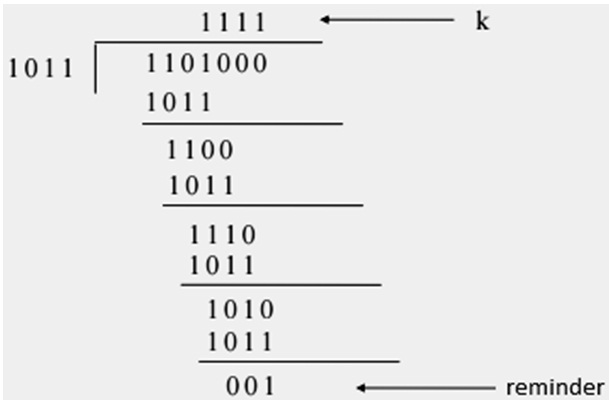
CRC Code Generation

Based on the desired number of bit checks, we will add some zeros (0) to the actual data. This new binary data sequence is divided by a new word of length n + 1, where n is the number of check bits to be added . The reminder obtained as a result of this modulo 2- division is added to the dividend bit sequence to form the cyclic code. The generated code word is completely divisible by the divisor that is used in generation of code. This is transmitted through the transmitter.

Example

At the receiver side, we divide the received code word with the same divisor to get the actual code word. For an error free reception of data, the reminder is 0. If the reminder is a non – zero, that means there is an error in the received code / data sequence. The probability of error detection depends upon the number of check bits (n) used to construct the cyclic code. For single bit and two bit errors, the probability is 100 % .

For a burst error of length n – 1, the probability of error detecting is 100 % .

A burst error of length equal to n + 1 , the probability of error detecting reduces to 1 – (1/2)^n-1 .

A burst error of length greater than n – 1 , the probability of error detecting is 1 – (1/2)ⁿ .

Back to top

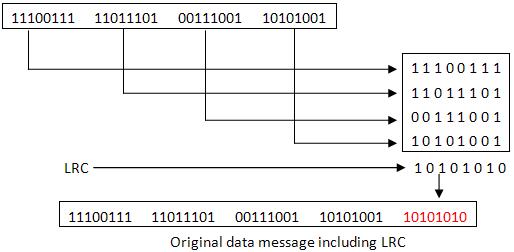
 Longitudinal Redundancy Check

In longitudinal redundancy method, a BLOCK of bits are arranged in a table format (in rows and columns) and we will calculate the parity bit for each column separately. The set of these parity bits are also sent along with our original data bits.

Longitudinal redundancy check is a bit by bit parity computation, as we calculate the parity of each column individually.

This method can easily detect burst errors and single bit errors and it fails to detect the 2 bit errors occurred in same vertical slice.

Back to top

Check Sum

Checksums are similar to parity bits except, the number of bits in the sums is larger than parity and the result is always constrained to be zero. That means if the checksum is zero, error is detected. A checksum of a message is an arithmetic sum of code words of certain length. The sum is stated by means of 1’s compliment and stored or transferred as a code extension of actual code word. At receiver a new checksum is calculated by receiving the bit sequence from transmitter.

The checksum method includes parity bits, check digits and longitudinal redundancy check (LRC). For example, if we have to transfer and detect errors for a long data sequence (also called as Data string) then we divide that into shorter words and we can store the data with a word of same width. For each another incoming bit we will add them to the already stored data. At every instance, the newly added word is called “Checksum”.

At receiver side, the received bits checksum is same as that of transmitter’s, there is no error found.

We can also find the checksum by adding all data bits. For example, if we have 4 bytes of data as 25h, 62h, 3fh, 52h.

Then, adding all bytes we get 118H

Dropping the carry Nibble, we get 18H

Find the 2’s complement of the nibble, i.e. E8H

This is the checksum of the transmitted 4 bits of data.

At receiver side,to check whether the data is received without error or not, just add the checksum to the actual data bits (we will get 200H). By dropping the carry nibble we get 00H. This means the checksum is constrained to zero. So there is no error in the data.

In general, there are 5 types of checksum methods like

• Integer addition checksum
• One’s complement checksum
• Fletcher Checksum
• Adler Checksum
• ATN Checksum (AN/466)

Example

As of now we discussed about the error detection codes. But to receive the exact and perfect data sequence without any errors, is not done enough only by detecting the errors occurred in the data. But also we need to correct the data by eliminating the presence of errors, if any. To do this we use some other codes.

Back to top

Error Correcting Codes

The codes which are used for both error detecting and error correction are called as “Error Correction Codes”. The error correction techniques are of two types. They are,

• Single bit error correction
• Burst error correction

The process or method of correcting single bit errors is called “single bit error correction”. The method of detecting and correcting burst errors in the data sequence is called “Burst error correction”.

Hamming code or Hamming Distance Code is the best error correcting code we use in most of the communication network and digital systems.

Back to top

Hamming Code

This error detecting and correcting code technique is developed by R.W.Hamming . This code not only identifies the error bit, in the whole data sequence and it also corrects it. This code uses a number of parity bits located at certain positions in the codeword. The number of parity bits depends upon the number of information bits. The hamming code uses the relation between redundancy bits and the data bits and this code can be applied to any number of data bits.

What  is a Redundancy Bit?

Redundancy means “The difference between number of bits of the actual data sequence and the transmitted bits”. These redundancy bits are used in communication system to detect and correct the errors, if any.

How the Hamming code actually corrects the errors?

In Hamming code, the redundancy bits are placed at certain calculated positions in order to eliminate errors. The distance between the two redundancy bits is called “Hamming distance”.

To understand the working and the data error correction and detection mechanism of the hamming code, let’s see to the following stages.

Number of parity bits

As we learned earlier, the number of parity bits to be added to a data string depends upon the number of information bits of the data string which is to be transmitted. Number of parity bits will be calculated by using the data bits. This relation is given below.

2^P >= n + P +1

Here, n represents the number of bits in the data string.

P represents number of parity bits.

For example, if we have 4 bit data string, i.e. n = 4, then the number of parity bits to be added can be found by using trial and error method. Let’s take P = 2, then

2^P = 2² = 4 and n + P + 1 = 4 + 2 + 1 = 7

This violates the actual expression.

So let’s try P = 3, then

2^P = 2³ = 8 and n + P + 1 = 4 + 3 + 1 = 8

So we can say that 3 parity bits are required to transfer the 4 bit data with single bit error correction.

Where to Place these Parity Bits?

After calculating the number of parity bits required, we should know the appropriate positions to place them in the information string, to provide single bit error correction.

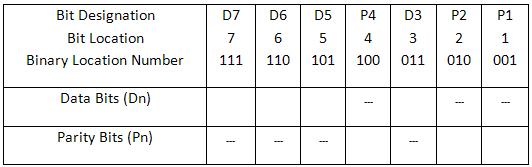
In the above considered example, we have 4 data bits and 3 parity bits. So the total codeword to be transmitted is of 7 bits (4 + 3). We generally represent the data sequence from right to left, as shown below.

bit 7, bit 6, bit 5, bit 4, bit 3, bit 2, bit 1, bit 0

The parity bits have to be located at the positions of powers of 2. I.e. at 1, 2, 4, 8 and 16 etc. Therefore the codeword after including the parity bits will be like this

D7, D6, D5, P4, D3, P2, P1

Here P1, P2 and P3 are parity bits. D1 —- D7 are data bits.

Constructing a Bit Location Table

In Hamming code, each parity bit checks and helps in finding the errors in the whole code word. So we must find the value of the parity bits to assign them a bit value.

By calculating and inserting the parity bits in to the data bits, we can achieve error correction through Hamming code.

Let’s understand this clearly, by looking into an example.

Ex:

Encode the data 1101 in even parity, by using Hamming code.

Step 1

Calculate the required number of parity bits.

Let P = 2, then

2^P = 2² = 4 and n + P + 1 = 4 + 2 + 1 = 7.

2 parity bits are not sufficient for 4 bit data.

So let’s try P = 3, then

2^P = 2³ = 8 and n + P + 1 = 4 + 3 + 1 = 8

Therefore 3 parity bits are sufficient for 4 bit data.

 The total bits in the code word are 4 + 3 = 7

Step 2

Constructing bit location table

Step 3

Determine the parity bits.

For P1 : 3, 5 and 7 bits are having three 1’s so for even parity, P1 = 1.

For P2 : 3, 6 and 7 bits are having two 1’s so for even parity, P2 = 0.
For P3 : 5, 6 and 7 bits are having two 1’s so for even parity, P3 = 0.

By entering / inserting the parity bits at their respective positions, codeword can be formed and is transmitted. It is 1100101.

NOTE: If the codeword has all zeros (ex: 0000000), then there is no error in Hamming code.

To represent the binary data in alphabets and numbers, we use alphanumeric codes.

Back to top

Alpha Numeric Codes

Alphanumeric codes are basically binary codes which are used to represent the alphanumeric data. As these codes represent data by characters, alphanumeric codes are also called “Character codes”.

These codes can represent all types of data including alphabets, numbers, punctuation marks and mathematical symbols in the acceptable form by computers. These codes are implemented in I/O devices like key boards, monitors, printers etc.
In earlier days, punch cards are used to represent the alphanumeric codes.

They are

•  MORSE code
•  BAUDOT code
• HOLLERITH code
•  ASCII code
•  EBCDI code
•  UNICODE

MORSE Code

At the starting stage of computer and digital electronics era, Morse code is very popular and most used code. This was invented by Samuel F.B.Morse, in 1837. It was the first ever telegraphic code used in telecommunication. It is mainly used in Telegraph channels, Radio channels and in air traffic control units.

BOUDOT Code

This code is invented by a French Engineer Emile Baudot, in 1870. It is a 5 unit code, means it uses 5 elements to represent an alphabet. It is also used in Telegraph networks to transfer Roman numeric.

HOLLERITH Code

This code is developed by a company founded by Herman Hollerith in 1896. The 12 bit code used to punch cards according to the transmitting information is called “Hollerith code”.

ASCII CODE

ASCII means American Standard Code for Information Interchange. It is the world’s most popular and widely used alphanumeric code. This code was developed and first published in 1967. ASCII code is a 7 bit code that means this code uses 27 = 128 characters. This includes

26 lower case letters (a – z), 26 upper case letters (A – Z), 33 special characters and symbols (like ! @ # $ etc), 33 control characters (* – + / and % etc) and 10 digits (0 – 9).

In this 7 bit code we have two parts, the leftmost 3 bits and right side 4 bits. The left most 3 bits are known “ZONE bits” and the right side 4 bits are known as “NUMERIC bits”

The 8 bit ASCII code can represent 256 (28) characters. It is called USACC – II or ASCII – 8 codes.

Example:

If we want to print the name LONDAN, the ASCII code is?

The ASCII-7 equivalent of L = 100 1100

The ASCII-7 equivalent of O = 100 1111

The ASCII-7 equivalent of N = 100 1110

The ASCII-7 equivalent of D = 100 0100

The ASCII-7 equivalent of A = 100 0001

The ASCII-7 equivalent of N = 100 1110

The output of LONDAN in ASCII code is 1 0 0 1 1 0 0 1 0 0 1 1 1 1 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0.

UNICODE

The draw backs in ASCII code and EBCDI code are that they are not compatible to all languages and they do not have sufficient set of characters to represent all types of data. To overcome these drawback this UNICODE is developed.
UNICODE is the new concept of all digital coding techniques. In this we have a different character to represent every number. It is the most advanced and sophisticated language with the ability to represent any type of data. SO this is known as “Universal code”. It is a 16 bit code, with which we can represent 216 = 65536 different characters.
UNICODE is developed by the combined effort of UNICODE consortium and ISO (International organization for Standardization).

EBCDI CODE

EBCDI stands for Extended Binary Coded Decimal Interchange code. This code is developed by IBM Inc Company. It is an 8 bit code, so we can represent 28 = 256 characters by using EBCDI code. This include all the letters and symbols like 26 lower case letters (a – z), 26 upper case letters (A – Z), 33 special characters and symbols (like ! @ # $ etc), 33 control characters (* – + / and % etc) and 10 digits (0 – 9).

In the EBCDI code, the 8 bit code the numbers are represented by 8421 BCD code preceded by 1111.

Back to top