In this tutorial, we will learn about one of the basic requirements of digital electronics i.e., the Binary Codes of the Binary Number System. Some of the popular Binary Codes are BCD (8421), 2421, 5211, Excess-3, Gray.
Outline
ToggleDifferent Types of Binary Codes
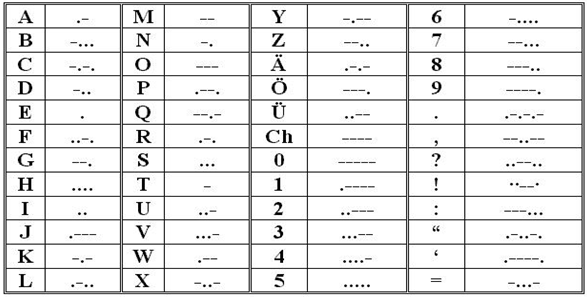
The first successful system of electrical communication was the telegraph, which was invented by Samuel F.B. Morse in the year 1832. The telegraph operators used a code of clicks to send the messages. If the key pressed for a short time it is the Morse code called ‘dot’ and if the key pressed for a long-time it is ‘Dash’. A sample Morse code is shown below:
If it is observed logically, various innumerable combinations of dots and dashes of any kind of words (even sentences) can be written utilizing the above code. In the same way, binary digits also be utilized to make such various innumerable combinations. These may be considered as Binary Codes.
Other than the commonly used 8421 code or BCD code, other Binary Codes like 2421 code, 5211 code, reflective code, sequential code, non-weighted code, excess-3 code and Gray code are also popular.
Commonly used Binary Codes
Before going into the details of individual binary codes, let us quickly take a look at some of the commonly used Binary Codes. The following is the list:
- 8421 Codes
- 2421 Codes
- 5211 Codes
- Excess-3 Codes
- Gray Codes
In the above list, the first three i.e., 8421, 2421 and 5211 are Weighted Binary Codes while the other two are Non-Weighted Binary Codes.
Weighted Binary Systems
The values assigned to consecutive places in the decimal system which is a place value system are 10⁴, 10³, 10², 10¹, 10⁰, 10⁻¹, 10⁻², 10⁻³… and so on from left to right. It is easily can be understood that the weight of digit of the decimal system is ‘10’.
For example:
(3546.25)10 = 3 x 10³ + 5 x 10² + 4 x 10¹ + 6 x 10⁰ + 2 x 10⁻¹ + 5 x 10⁻²
In the same way, the values assigned to consecutive places in the binary system, which is also a place value system, are called as weighted binary system.
The weights in a binary system are 2⁴, 2³, 2², 2¹, 2⁰, 2⁻¹, 2⁻², 2⁻³… from left to right. It is easily can be understood that the weight of digit of the binary system is ‘2’.
For example:
(1110110)2 = 1 x 2⁶+ 1 x 2⁵ + 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2⁰
= 64 + 32 + 16 + 0 + 4 + 2 + 0 = (118)10
Binary Weights
Whenever any binary number appears, its decimal equivalent can be found easily as follows.
- When there is 1 in a digit position, weight of that position should be added.
- When there is 0 in a digit position, weight of that position should be disregarded.
For example binary number 1100 has a decimal equivalent of 8 + 4 + 0 + 0 = 12.
8421 Code or BCD Code
The decimal numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 can be expressed in Binary numbers as shown in the following table. All these binary numbers again expressed in the last column by expanding into 4 bits. As per the weighted binary digits, the 4 Bit binary numbers can be expressed according to their place value from left to right as 8421 (2³ 2² 2¹ 2⁰ = 8421).
As per the above expression all the decimal numbers written in the 4 Bit binary code in the form of 8421 and this is called as 8421 Code and also as Binary coded decimal BCD.
As this is a straight code, any Decimal number can be expressed easily because the weights of the positions are straight for easy conversion into this 8421 code.
There are other forms of codes which are not so popular but rather confusing. They are 2421 code, 5211 code, reflective code, sequential code, non- weighted coded, excess-3 code and Grey code. They are having their own importance for some of the exclusive applications and may be useful for some of the special applications.
2421 Code
This code also a 4 bit application code where the binary weights carry 2, 4, 2, 1 from left to right.
5211 Code
This code is also a 4 bit application code where the binary weights carry 5, 2, 1, 1 from left to right.
Reflective Code
It can be observed that in the 2421 and 5211 codes, the code for decimal 9 is the complement of the code for decimal 0, the code for decimal 8 is the complement of the code for decimal 1, the code for decimal 7 is the complement of the code for decimal 2, the code for decimal 6 is the complement of the code for decimal 3, the code for decimal 5 is the complement of the code for decimal 4. These codes are called as Reflective Codes. The same can be observed in the following table:
NOTE: 8421 code is not a reflective code.
Sequential Codes
Sequential codes are the codes in which 2 subsequent numbers in binary representation differ by only one digit. The 8421 and Excess-3 codes are examples of sequential codes. 2421 and 5211 codes do not come under sequential codes.
Non-Weighted Codes
Some of the codes will not follow the weights of the sequence binary numbers these are called as non-weighted codes. ASCII code and Grey code are some of the examples where they are coded for some special purpose applications and they do not follow the weighted binary number calculations.
Excess-3 Code
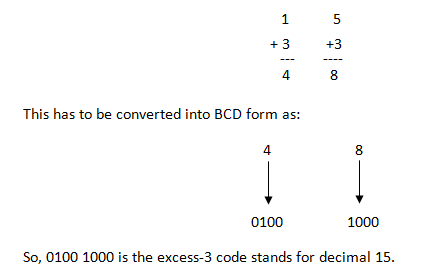
As mentioned above, some of the codes will not follow the binary weights, Excess-3 code is an example of it and it is an important 4 bit code. The excess – 3 code of a decimal number is achieved by adding the number 3 to the 8421 code.
For example to convert 15 to an excess-3 code, first 3 to be added to each digit as shown below.
Excess – 3 Code Examples
- Find the excess-3 code of (237.75)10
- Find the decimal number of excess-3 number 110010100011.01110101.
Sol:
1) The excess-3 code for (237)10 is obtained by adding 3 to all the digits individually, that is 2, 3 and 7 will become 5, 6 and 10 respectively. These 5, 6 and 10 decimals have to be converted into binary form and the result is 010101101010.
The excess-3 code for (.75)10 is obtained by replacing 7 and 5 with 10 and 8 respectively by adding 3 to each digit. That is, the excess-3 code for (.75)10 is .10101000.
Combining the results of the integral and fractional parts, the excess-3 code for (237.75)10 is 010101101010.10101000.
2) The excess-3 code is 110010100011.01110101
By separating 4 bits as group the equivalent excess-3 code is given as 1100 1010 0011.0111 0101.
Subtracting 0011 from each four-bit group, we obtain the new number as: 1001 0111 0000.0100 0010.
Therefore, the decimal equivalent is (970.42)10.
Gray Code
The gray code is the code where one bit will be differed to the preceding number. For example, decimal numbers 13 and 14 are represented by gray code numbers 1011 and 1001, these numbers differ only in single position that is the second position from the right. In the same way first position on the left changes for 7 and 8 which are 0100 and 1100 and this is also called Unit-distance code. The gray code has very special place in digital electronics.
Conclusion
An introductory tutorial on Binary Codes. You learned different binary codes like BCD (8421), 2421, 5211, Excess-3 and Gray Codes.


4 Responses
Nicely explain ….good job
Really helpful. Thanks 🙂
nice explanation
Good article, just one minor correction. You listed the weights as 5, 4, 2 and 1 for 5211 code, when they are really 5, 2, 1 and 1.