In this tutorial, we will learn about Wheatstone Bridge. We will see the Working principle of Wheatstone Bridge, few example circuits and some important applications.
Outline
ToggleResistance Measurement and Its Types
In the World of analog electronics, we come across various signals, some of them are measured by changes in resistance and some of them are with changes in inductance and capacitance.
If we consider the resistance, most of the industrial sensors like temperature, strain, humidity, displacement, liquid level, etc. produces the change in value of the resistance for an equivalent change in the respective quantity. Therefore, there is a need for a signal conditioning for every resistance based sensor.
For example, the simplest device we can think of is the Light Dependent Resistor or LDR. As the name suggests, an LDR is a device, whose resistance changes according to the amount of light falling on it.
Generally, the resistance measurement is divided into three types:
- Low Resistance Measurement
- Medium Resistance Measurement
- High Resistance Measurement
If the resistance measurement is possibly from a few micro ohms to milli ohms, then it is considered as a low resistance measurement. This measurement is actually used for research purpose. If the measurement is from 1 ohm to few hundreds of KΩ is generally referred as a medium resistance measurement. Measurement of normal resistors, potentiometers, thermistors, etc. comes under this category.
And very high resistance measurement is considered from few Mega Ohms to greater than 100 Mega Ohms. For finding the medium value of the resistance different methods are used, but mostly Wheatstone bridge is used.
What is Wheatstone Bridge?
Bridge Networks or Circuits are one of the most popular and popular electrical tools, often used in measurement circuits, transducer circuits, switching circuits and also in oscillators.
The Wheatstone Bridge is one of the most common and simplest bridge network / circuit, which can be used to measure resistance very precisely. But often the Wheatstone Bridge is used with Transducers to measure physical quantities like Temperature, Pressure, Strain etc.
Wheatstone Bridge is used in applications where small changes in resistance are to be measured in sensors. This is used to convert a change in resistance to a change in voltage of a transducer. The combination of this bridge with operational amplifier is used extensively in industries for various transducers and sensors.
For example, the resistance of a Thermistor changes when it is subjected to change in temperature. Likewise, a strain gauge, when subjected to pressure, force or displacement, its resistance changes. Depending on the type of application, the Wheatstone Bridge can be operated either in a Balanced condition or an Unbalanced condition.
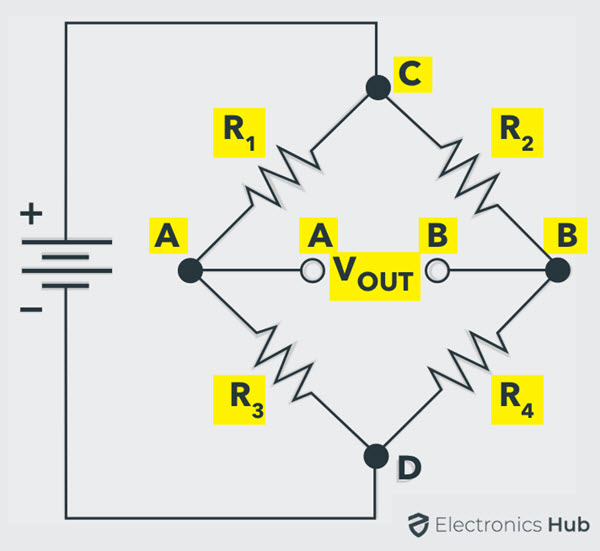
A Wheatstone bridge consists of four resistors (R1, R2, R3 and R4) that are connected in the shape of a diamond with the DC supply source connected across the top and bottom points (C and D in the circuit) of the diamond and the output is taken across the other two ends (A and B in the circuit).
This bridge is used to find the unknown resistance very precisely by comparing it with a known value of resistances. In this bridge, a Null or Balanced condition is used to find the unknown resistance.
For this bridge to be in a Balanced Condition, the output voltage at points A and B must be equal to 0. From the above circuit:
The Bridge is in Balanced Condition if:
VOUT = 0 V
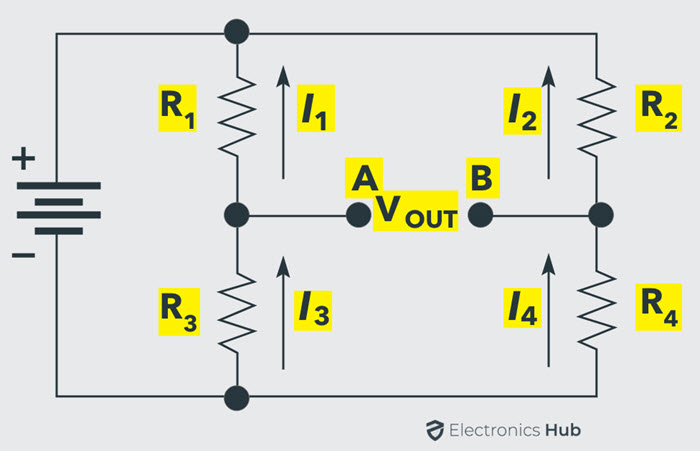
To simplify the analysis of the above circuit, let us redraw it as follows:
Now, for Balanced Condition, the voltage across the resistors R1 and R2 is equal. If V1 is the voltage across R1 and V2 is the voltage across R2, then:
V1 = V2
Similarly, the voltage across resistors R3 (let us call it V3) and R4 ( let us call it V4) are also equal. So,
V3 = V4
The ratios of the voltage can be written as:
V1 / V3 = V2 / V4
From Ohm’s law, we get:
I1 R1 / I3 R3 = I2 R2 / I4 R4
Since I1 = I3 and I2 = I4, we get:
R1 / R3 = R2 / R4
From the above equation, if we know the values of three resistors, we can easily calculate the resistance of the fourth resistor.
Alternative Way to Calculate Resistors
From the redrawn circuit, if VIN is the input voltage, then the voltage at point A is:
VIN ( R3 / (R1 + R3))
Similarly, the voltage at point B is:
VIN ( R4 / (R2 + R4))
For the Bridge to be Balanced, VOUT = 0. But we know that VOUT = VA – VB .
So, in Balanced Bridge Condition,
VA = VB
Using above equations, we get:
VIN ( R3 / (R1 + R3)) = VIN ( R4 / (R2 + R4))
After simple manipulation of the above equation, we get:
R1 / R3 = R2 / R4
From the above equation, if R1 is an unknown resistor, its value can be calculated from the known values of R2, R3 and R4. Generally, the unknown value is called as RX and of the three known resistances, one resistor (mostly R3 in the above circuit) is usually a variable Resistor called as RV.
Find Unknown Resistance using Balanced Wheatstone Bridge
In the above circuit, let us assume that R1 is an unknown resistor. So, let us call it RX. The resistors R2 and R4 have a fixed value. Which means, the ratio R2 / R4 is also fixed. Now, from the above calculation, to create a balanced condition, the ratio of resistors must be equal i.e.,
RX / R3 = R2 / R4
Since the ratio R2 / R4 is fixed, we can easily adjust the other known resistor (R3) to achieve the above condition. Hence, it is important that R3 is a variable resistor, which we call RV.
But how do we detect the Balanced Condition? This is where a Galvanometer (an old school Ammeter) can be used. By placing the Galvanometer between the points A and B, we can detect the Balanced Condition.
With RX placed in the circuit, adjust the RV until the Galvanometer points to 0. At this point, note down the value of RV. By using the following formula, we can calculate the unknown resistor RX.
RX = RV (R2 / R4)
Unbalanced Wheatstone Bridge
If VOUT in the above circuit is not equal to 0 (VOUT ≠ 0), the Wheatstone is said to be an Unbalanced Wheatstone Bridge. Usually, the Unbalanced Wheatstone Bridge is often used for measurement of different physical quantities like Pressure, Temperature, Strain etc.
For this to work, the Transducer must be of resistive type i.e., the resistance of the transducer changes appropriately when the quantity it is measuring (temperature, strain, etc.) changes. In place of unknown resistor in the previous resistance calculation example, we can connect the transducer.
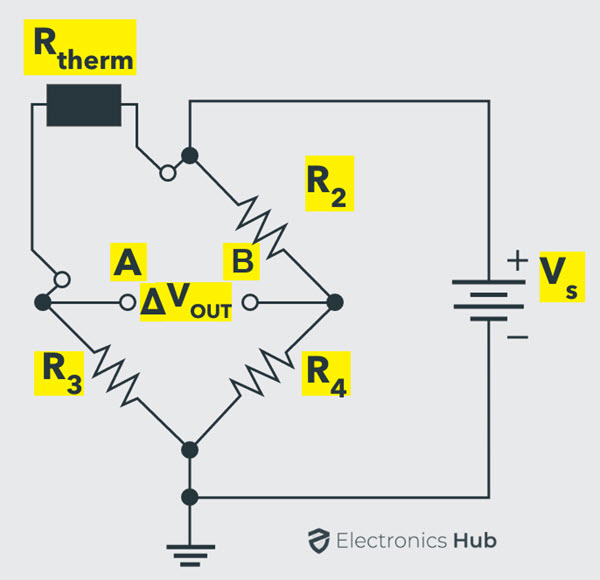
Wheatstone Bridge for Temperature Measurement
Let us now see how we can measure temperature using an unbalanced Wheatstone Bridge. The transducer which we are going to use here is called a Thermistor, which is a temperature dependent resistor. Depending on the temperature co-efficient of the thermistor, changes in temperature will either increase or decrease the resistance of the thermistor.
As a result, the output voltage of the Bridge VOUT will become a non-zero value. This means that the output voltage VOUT is proportional to the temperature. By calibrating the voltmeter, we can display the temperature in terms of the output voltage.
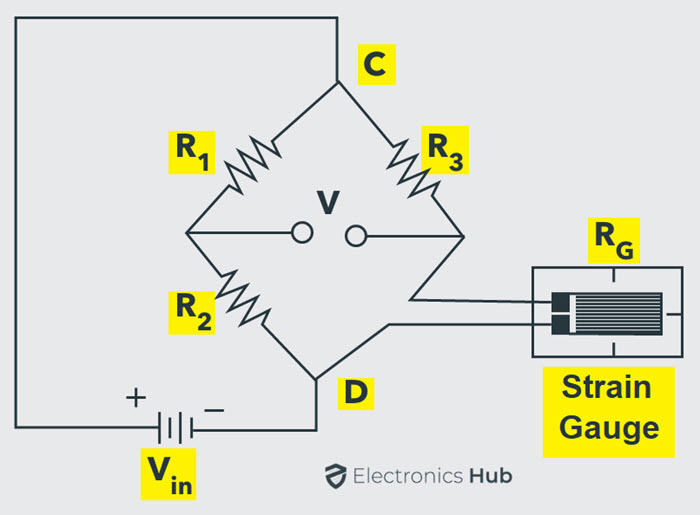
Wheatstone Bridge for Strain Measurement
One of the most commonly used applications of Wheatstone Bridge is in the Strain Measurement. Strain Gauge is a device whose electrical resistance varies in proportion to the mechanical factors like Pressure, Force or Strain.
Usually, the range of strain gauge resistance is from 30 Ω to 3000 Ω. For a given strain, the resistance change may be only a fraction of the full range. Therefore, to accurately measure the fractional changes of resistance, a Wheatstone Bridge configuration is used.
The circuit below shows a Wheatstone bridge where the unknown resistor is replaced with a strain gauge.
Due to the external force, the resistance of the strain gauge changes and as a result, the bridge becomes unbalanced. The output voltage can be calibrated to display the changes in strain.
One popular configuration of Strain Gauges and Wheatstone Bridge is in Weight Scales. In this, the Strain Gauges are carefully mounted as a single unit called as Load Cells, which is a transducer which converts mechanical force to electrical signal.
Usually, weight scales consist of four load cells, where two strain gauges expand or stretch (tension type) when external force is acting and two strain gauges compress (compression type) when load is placed.
If the strain gauge is either tensed or compressed, then the resistance can increase or decrease. Therefore, this causes unbalancing of the bridge. This produces a voltage indication on voltmeter corresponds to the strain change. If the strain applied on a strain gauge is more, then the voltage difference across the meter terminals is more. If the strain is zero, then the bridge balances and the meter shows zero reading.
This is about the resistance measurement using a Wheatstone bridge for precise measurement. Due to the fractional measurement of resistance, Wheatstone bridges are mostly used in strain gauge and thermometer measurements.
Applications
- The Wheatstone Bridge is used for measuring the very low resistance values precisely.
- Wheatstone bridge along with operational amplifier is used to measure the physical parameters like temperature, strain, light, etc.
- We can also measure the quantities capacitance, inductance and impedance using the variations on the Wheatstone Bridge.
Conclusion
A beginner’s guide on Wheatstone Bridge. You learned What is a Wheatstone Bridge Circuit, what is the meaning of a Balanced Bridge, how to calculate an unknown resistance using Wheatstone Bridge and also how an Unbalanced Wheatstone Bridge can be used to measure different physical quantities like Temperature and Strain.



4 Responses
Which circuit is used to increase the output voltage of Wheatstone’s bridge?
You can cascade a differential op amp to amplify the output voltage.
Which bridge would you prefer to use for the measurement of a test resistor having a value around 50 k Ω ?
How does the inaccuracy in the value of the known resistance affect the accuracy of the result