Boolean Logic in SOP (Sum of Products) and POS (Product of Sums) forms is foundational to digital circuit design, providing a systematic way of expressing and simplifying logical expressions. SOP form combines multiple OR operations applied to ANDed terms, whereas POS form involves AND operations applied to ORed terms, each efficiently representing complex logic circuits. These forms are pivotal in optimizing digital systems for both hardware efficiency and computational speed, serving as the cornerstone for understanding and implementing digital logic in various applications.
Outline
ToggleBoolean Expression Logic Representation
The use of switching devices like transistors give rise to a special case of the Boolean algebra called as switching algebra. In switching algebra, all the variables assume one of the two values which are 0 and 1.
- In Boolean algebra, 0 is used to represent the ‘open’ state or ‘false’ state of logic gate. Similarly, 1 is used to represent the ‘closed’ state or ‘true’ state of logic gate.
- A Boolean expression is an expression which consists of variables, constants (0-false and 1-true) and logical operators which results in true or false.
- A Boolean function is an algebraic form of Boolean expression. A Boolean function of n-variables is represented by f(x1, x2, x3….xn). By using Boolean laws and theorems, we can simplify the Boolean functions of digital circuits. A brief note of different ways of representing a Boolean function is shown below.
- Sum-of-Products (SOP) Form
- Product-of-sums (POS) form
- Canonical forms
There are two types of canonical forms:
- Sum-of-min terms or Canonical SOP
- Product-of- max terms or Canonical POS
Boolean functions can be represented by using NAND gates and also by using K-map (Karnaugh map) method. We can standardize the Boolean expressions by using by two standard forms.
- SOP form – Sum Of Products form
- POS form – Product Of Sums form
Standardization of Boolean equations will make the implementation, evolution and simplification easier and more systematic.
Sum of Product (SOP) Form
The sum-of-products (SOP) form is a method (or form) of simplifying the Boolean expressions of logic gates. In this SOP form of Boolean function representation, the variables are operated by AND (product) to form a product term and all these product terms are ORed (summed or added) together to get the final function.
A sum-of-products form can be formed by adding (or summing) two or more product terms using a Boolean addition operation. Here the product terms are defined by using the AND operation and the sum term is defined by using OR operation.
The sum-of-products form is also called as Disjunctive Normal Form as the product terms are ORed together and Disjunction operation is logical OR. Sum-of-products form is also called as Standard SOP.
SOP form representation is most suitable to use them in FPGA (Field Programmable Gate Arrays).
SOP Form Examples
AB + ABC + CDE
(AB) ̅ + ABC + CD E ̅
SOP form can be obtained by
- Writing an AND term for each input combination, which produces HIGH output.
- Writing the input variables if the value is 1, and write the complement of the variable if its value is 0.
- OR the AND terms to obtain the output function.
Ex: Boolean expression for majority function F = A’BC + AB’C + ABC ‘ + ABC
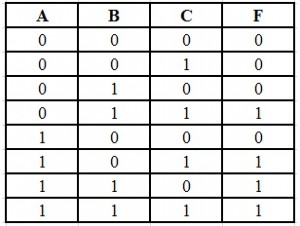
SOP Form Truth Table:
Now write the input variables combination with high output. F = AB + BC + AC.
Checking
By Idempotence law, we know that
([ABC + ABC)] + ABC) = (ABC + ABC) = ABC
Now the function F = A’BC + AB’C + ABC ‘ + ABC
= A’BC + AB’C + ABC’ + ([ABC + ABC)] + ABC)
= (ABC + ABC ‘) + (ABC + AB’C) + (ABC + A’BC)
= AB (C + C ‘) + A (B + B’) C + (A + A’) BC
= AB + BC + AC.
Product of Sums (POS) Form
The product of sums form is a method (or form) of simplifying the Boolean expressions of logic gates. In this POS form, all the variables are ORed, i.e. written as sums to form sum terms.
All these sum terms are ANDed (multiplied) together to get the product-of-sum form. This form is exactly opposite to the SOP form. So this can also be said as “Dual of SOP form”.
Here the sum terms are defined by using the OR operation and the product term is defined by using AND operation. When two or more sum terms are multiplied by a Boolean OR operation, the resultant output expression will be in the form of product-of-sums form or POS form.
The product-of-sums form is also called as Conjunctive Normal Form as the sum terms are ANDed together and Conjunction operation is logical AND. Product-of-sums form is also called as Standard POS.
POS Form Examples
(A+B) * (A + B + C) * (C +D)
(A+B) ̅ * (C + D + E ̅)
POS form can be obtained by
- Writing an OR term for each input combination, which produces LOW output.
- Writing the input variables if the value is 0, and write the complement of the variable if its value is 1.
- AND the OR terms to obtain the output function.
Ex: Boolean expression for majority function F = (A + B + C) (A + B + C ‘) (A + B’ + C) (A’ + B + C)
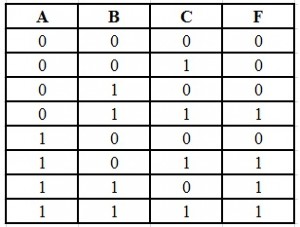
POS Form Truth Table:
Now write the input variables combination with high output. F = AB + BC + AC.
Checking
By Idempotence law, we know that
[(A + B + C) (A + B + C)] (A + B + C) = [(A + B + C)] (A + B + C) = (A + B + C)
Now the function
F = (A + B) (B + C) (A + C)
= (A + B + C) (A + B + C ‘) (A + B’ + C) (A’ + B + C)
= [(A + B + C) (A + B + C)] (A + B + C) (A + B + C ‘) (A + B’ + C) (A’ + B + C)
= [(A + B + C) (A + B + C ‘)] [(A + B + C) (A’ + B + C)] [(A + B + C) (A + B’ + C)]
= [(A + B) + (C * C ‘)] [(B + C) + (A * A’)] [(A + C) + (B * B’)]
= [(A + B) + 0] [(B + C) + 0] [(A + C) + 0] = (A + B) (B + C) (A + C)
Canonical Form (Standard SOP and POS Form)
Any Boolean function that is expressed as a sum of minterms or as a product of max terms is said to be in its “canonical form”.
It mainly involves in two Boolean terms, “minterms” and “maxterms”.
When the SOP form of a Boolean expression is in canonical form, then each of its product term is called ‘minterm’. So, the canonical form of sum of products function is also known as “minterm canonical form” or Sum-of-minterms or standard canonical SOP form.
Similarly, when the POS form of a Boolean expression is in canonical form, then each of its sum term is called ‘maxterm’. So, the canonical form of product of sums function is also known as “maxterm canonical form or Product-of sum or standard canonical POS form”.
Min terms
A minterm is defined as the product term of n variables, in which each of the n variables will appear once either in its complemented or un-complemented form. The min term is denoted as mi where i is in the range of 0 ≤ i < 2ⁿ.
A variable is in complemented form, if its value is assigned to 0, and the variable is un-complimented form, if its value is assigned to 1.
For a 2-variable (x and y) Boolean function, the possible minterms are:
x’y’, x’y, xy’ and xy.
For a 3-variable (x, y and z) Boolean function, the possible minterms are:
x’y’z’, x’y’z, x’yz’, x’yz, xy’z’, xy’z, xyz’ and xyz.
- 1 – Minterms = minterms for which the function F = 1.
- 0 – Minterms = minterms for which the function F = 0.
Any Boolean function can be expressed as the sum (OR) of its 1- min terms. The representation of the equation will be
- F(list of variables) = Σ(list of 1-min term indices)
Ex: F (x, y, z) = Σ (3, 5, 6, 7)
The inverse of the function can be expressed as a sum (OR) of its 0- min terms. The representation of the equation will be
- F(list of variables) = Σ(list of 0-min term indices)
Ex: F’ (x, y, z) = Σ (0,1, 2, 4)
Examples of canonical form of sum of products expressions (min term canonical form):
i) Z = XY + XZ′
ii) F = XYZ′ + X′YZ + X′YZ′ + XY′Z + XYZ
In standard SOP form, the maximum possible product terms for n number of variables are given by 2ⁿ. So, for 2 variable equations, the product terms are 22 = 4. Similarly, for 3 variable equations, the product terms are 23 = 8.
Max terms
A max term is defined as the product of n variables, within the range of 0 ≤ i < 2ⁿ. The max term is denoted as Mi. In max term, each variable is complimented, if its value is assigned to 1, and each variable is un-complimented if its value is assigned to 0.
For a 2-variable (x and y) Boolean function, the possible max terms are:
x + y, x + y’, x’ + y and x’ + y’.
For a 3-variable (x, y and z) Boolean function, the possible maxterms are:
x + y + z, x + y + z’, x + y’ + z, x + y’ + z’, x’ + y + z, x’ + y + z’, x’ + y’ + z and x’ + y’ + z’.
- 1 – Max terms = max terms for which the function F = 1.
- 0 – max terms = max terms for which the function F = 0.
Any Boolean function can be expressed the product (AND) of its 0 – max terms. The representation of the equation will be
- F(list of variables) = Π (list of 0-max term indices)
Ex: F (x, y, z) = Π (0, 1, 2, 4)
The inverse of the function can be expressed as a product (AND) of its 1 – max terms. The representation of the equation will be
- F(list of variables) = Π (list of 1-max term indices)
Ex: F’ (x, y, z) = Π (3, 5, 6, 7)
Examples of canonical form of product of sums expressions (max term canonical form):
i. Z = (X + Y) (X + Y′)
ii. F = (X′ + Y + Z′) (X′ + Y + Z) (X′ + Y′ + Z′)
In standard POS form, the maximum possible sum terms for n number of variables are given by 2ⁿ. So, for 2 variable equations, the sum terms are 22 = 4. Similarly, for 3 variable equations, the sum terms are 23 = 8.
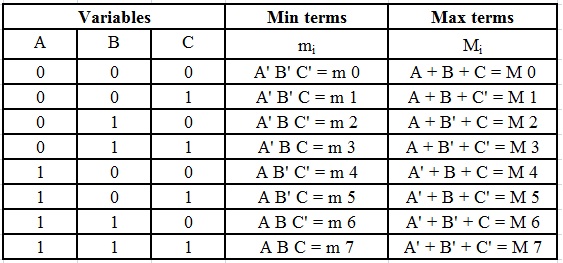
Table for 2n min terms and 2n max terms
The below table will make you understand about the representation of the mean terms and max terms of 3 variables.
Conversions of Canonical Forms
We can represent the one canonical formed equation in other canonical form i.e. we can represent the SOP form of equation in POS form and POS form equation in SOP form. To convert the canonical equations, we interchange the Σ and Π symbols after listing out the index numbers of the equations, which are excluded from the original form of equation.
The important thing to remember about Boolean functions is that, the SOP and POS forms are Duals to each other. There are 2 steps to follow to convert the canonical form of the equations. They are
Step 1: Interchanging the operational symbols, Σ and Π in the equation.
Step 2: Use the De Morgan’s principle of Duality to the index numbers of the Boolean function or writing the indexes of the terms that are not presented in the given form of equation.
Conversion of SOP form to POS form
To convert the SOP form into POS form, first we should change the Σ to Π and then write the numeric indexes of missing variables of the given Boolean function.
Example:
The SOP function
F = ∑ A, B, C (0, 2, 3, 5, 7) = A’ B’ C’ + A B’ C’ + A B’ C + ABC’ + ABC is written in POS form by
Step 1: changing the operational sign to Π
Step 2: writing the missing indexes of the terms, 001, 100 and 110. Now write the sum form for these noted terms.
001 = (A + B + C) 100 = (A + B’ + C’) 110 = (A + B’ + C’)
Writing down the new equation in the form of POS form,
F = Π A, B, C (1, 4, 6) = (A + B + C) * (A + B’ + C’) * (A + B’ + C’)
Conversion of POS form to SOP form
To convert the POS form into SOP form, first we should change the Π to Σ and then write the numeric indexes of missing variables of the given Boolean function.
Ex: The POS function F = Π A, B, C (2, 3, 5) = A B’ C’ + A B’ C + ABC’ is written in SOP form by
Step 1: changing the operational sign to Σ
Step 2: writing the missing indexes of the terms, 000, 001, 100, 110, and 111. Now write the product form for these noted terms.
000 = A’ * B’ * C’ 001 = A’ * B’ * C 100 = A * B’ * C’
110 = A * B* C’ 111 = A * B * C
Writing down the new equation in the form of SOP form,
F = Σ A, B, C (0, 1, 4, 6, 7) = (A’ * B’ * C’) + (A’ * B’ * C) + (A * B’ * C’) + (A * B* C’) + (A * B * C)
Conversion of SOP form to standard SOP form or Canonical SOP form
We can include all the variables in each product term of the SOP form equation, which doesn’t have all the variables by converting into standard SOP form. The normal SOP form function can be converted to standard SOP form by using the Boolean algebraic law, (A + A’ = 1) and by following the below steps.
Step 1:
By multiplying each non-standard product term with the sum of its missing variable and its complement, which results in 2 product terms
Step 2:
By repeating the step 1, until all resulting product terms contain all variables
By these two steps we can convert the SOP function into standard SOP function. In this process, for each missing variable in the function, the number of product terms will double.
Example:
Convert the non standard SOP function F = x y + x z + y z
Sol:
F = x y + x z + y z
= x y (z + z’) + x (y + y’) z + (x + x’) y z
= x y z + x y z’ + x y z + x y’ z + x y z + x’ y z
= x y z + x y z’ + x y’ z + x’ y z
The standard SOP form is F = x y z + x y z’ + x y’ z + x’ y z
Conversion of POS form to standard POS form or Canonical POS form
We can include all the variables in each product term of the POS form equation, which doesn’t have all the variables by converting into standard POS form. The normal POS form function can be converted to standard POS form by using the Boolean algebraic law, (A * A’ = 0) and by following the below steps.
Step 1:
By adding each non-standard sum term to the product of its missing variable and its complement, which results in 2 sum terms
Step 2:
Applying Boolean algebraic law, A + BC = (A + B) * (A + C)
Step 3:
By repeating the step 1, until all resulting sum terms contain all variables
By these three steps we can convert the POS function into standard POS function.
Example:
F = (A’ + B + C) * (B’ + C + D’) * (A + B’ + C’ + D)
In the first term, the variable D or D’ is missing, so we add D*D’ = 1 to it. Then
(A’ + B + C + D*D’) = (A’ + B + C + D) * (A’ + B + C + D’)
Similarly, in the second term, the variable A or A’ is missing, so we add A*A’ = 1 to it. Then
(B’ + C + D’ + A*A’) = (A + B’ + C + D’) * (A’ + B’ + C + D’)
The third term is already in the standard form, as it has all the variables. Now the standard POS form equation of the function is
F = (A’ + B + C + D) * (A’ + B + C + D’) * (A + B’ + C + D’) * (A’ + B’ + C + D’) * (A + B’ + C’ + D)


17 Responses
How to prove that sop=complement of pos
what is the need to convert sop to standard sop
What is diffrent of pos&sop?
pos stands for product of sum. for example:- (a+b).(b+c)
sop stands for sum of products. for example:- ab+bc
difference between SOP and POS is that the SOP is a way of representing a Boolean expression using min terms or product terms while the POS is a way of representing a Boolean expression using max terms or sum terms.
IN SOP WE TAKE (1) AS NONCOMPLEMENT AND (0) AS COMPLEMENT AND FULL FORM OF SOP IS SUM OF PRODUCT WHICH IS REPRESENT BY (m) minterm (A’.B.C’)
IN POS WE TAKE (0) AS NONCOMPLEMENT AND (1) AS COMPLEMENT AND FULLFORM OF
POS IS PRODUCT OF SUM WHICH IS REPRESENT BY (M) MAXTERM (A’+B’+C)
Take complement or bar of sop form then apply boolean logics and de-morgan’s theorem.
(AB+BC)’ = [ (AB)’ * (BC)’ ]
= [ (A’ + B’) * (B’ + C’) ]
( SOP )’ = POS
AS SIMILAR SOP = (POS)’
It also can be proven by truth table.
A B AB (A’+B’)’
0 0 0 0
0 1 0 0
1 0 0 0
1 1 1 1
its False
Example:
The SOP function
F = ∑ A, B, C (0, 2, 3, 5, 7) = A’ B’ C’ + A B’ C’ + A B’ C + ABC’ + ABC is written in POS form by
Step 1: changing the operational sign to Π
Step 2: writing the missing indexes of the terms, 001, 100 and 110. Now write the sum form for these noted terms.
001 = (A + B + C) 100 = (A + B’ + C’) 110 = (A + B’ + C’)
Writing down the new equation in the form of POS form,
F = Π A, B, C (1, 4, 6) = (A + B + C) * (A + B’ + C’) * (A + B’ + C’)
Answer this question
(a+b) (c+d’)
Convert a(b+c)(c+d) into canonical pos form
sop to pos conversion method is right but mistake in variables chosen
The SOP function
F = ∑ A, B, C (0, 2, 3, 5, 7) = A’ B’ C’ + A’ B C’ + A’ B C + AB’C + ABC is written in POS form by corrected by gautam rai
Step 1: changing the operational sign to Π
Step 2: writing the missing indexes of the terms, 001, 100 and 110. Now write the sum form for these noted terms.
001 = (A + B + C) 100 = (A + B’ + C’) 110 = (A + B’ + C’)
Writing down the new equation in the form of POS form,
F = Π A, B, C (1, 4, 6) = (A + B + C’) * (A’ + B’ + C) * (A’ + B + C) corrected by gautam
simplify boolean expression f(a,b,c)=sum(3,4,6,7) using kmap.
what is the uses of sop&pos
Convert the following into sop and pos forms : Y=A + AB + ABC
Please solve this expression with pos expression into cananonical expression : A(B+C’) (C’+D’)
What is the SOP and POS process of K-MAP