In this tutorial, we will learn about the Implementation of Boolean Functions using Logic Gates. In our previous tutorial, we learned about the Boolean Algebra Laws and associated theorems. We also learned that the Boolean Functions can be represented easily in SOP (sum of products) form and POS (product of sums) form. To represent these standardized equations logically, we use the logic gates.
Any Boolean function can be represented by using a number of logic gates by properly interconnecting them. Logic gates implementation or logic representation of Boolean functions is very simple and easy form.
The implementation of Boolean functions by using logic gates involves connecting output of one logic gate to the input of another gate. Commonly used Logic Gates are: AND, OR, NAND and NOR gates.
Let’s have a look into the logic gate implementation of SOP and POS forms of Boolean functions.
Outline
ToggleA Brief Introduction to Logic Gates
Logic Gates are the basic building blocks of digital electronic circuits. A Logic Gate is a piece of electronic circuit, that can be used to implement Boolean Expressions.
While Laws and Theorems of Boolean Logic are used to manipulate the Boolean Expressions, Logic Gates are used to implement these Boolean Expressions in Digital Electronics.
AND gate, OR gate and NOT gate are the three basic logic gates used in digital electronics. Using these basic logic gates, other Logic Gates like NAND, NOR, Exclusive OR (Ex-OR) and Exclusive NOR (Ex-NOR) are derived.
Before seeing the implementation of Boolean Functions using Logic Gates, let us quickly recap some basics about the important logic gates.
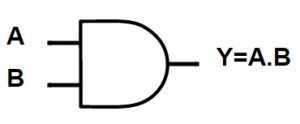
AND Gate
Logic AND gate is a basic logic gate, with two or more inputs and one output. The output of an AND gate is HIGH only if all the inputs of the gate are HIGH. The output for all the other cases of the inputs is LOW. The logic symbol and the truth table of an AND gate is shown below.
| A | B | Y = A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
If ‘A’ and ‘B’ are the two inputs of an AND Gate, the output expression is written as:
Y = A . B or Y = A B
It is read as “Y EQUALS A AND B”.
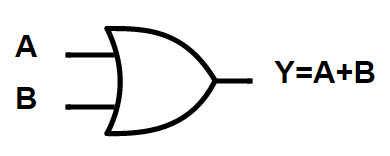
OR Gate
The OR Gate is used to preform logical ‘OR’ operation. OR Gate also contains two or more inputs and one output. The output of an OR gate is HIGH if either of the inputs are HIGH. The output is LOW when all the inputs are LOW. The logic symbol and the truth table of an OR gate is shown below.
| A | B | Y = A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
If ‘A’ and ‘B’ are the two inputs of an OR Gate, the output expression is written as:
Y = A + B
It is read as “Y EQUALS A OR B”.
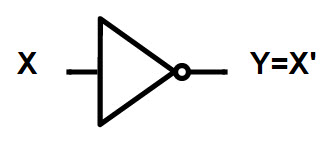
NOT Gate
Logic NOT gate is another basic logic gate with one input and one output. The output of the NOT Gate is always the complement of the input. If the input is HIGH, the output is LOW and if the input is LOW, the output is HIGH. The logic symbol and the truth table of a NOT gate is shown below.
| X | Y = X’ |
| 0 | 1 |
| 1 | 0 |
NOT Gate is used to produce the complement of a variable in Boolean Algebra. So, it is also called as Complementing or Inverting Circuit.
SOP Boolean Function Implementation using Logic Gates
The sum of product or SOP form is represented by using basic logic gates: AND gate and OR gate. The SOP form implementation will have AND gates at its input side and as the output of the function is the sum of all product terms, it has an OR gate at its output side.
An important to remember is that we use NOT gate to represent the inverse or complement of the variables.
| Sum of Products (SOP) | |
| Input | AND |
| Output | OR |
Implementation for 2 Input Variables
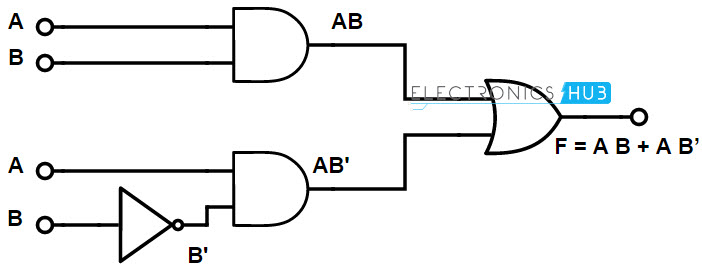
Let us understand how we can implement the following Boolean function using basic logic gates.
F = A B + A B
In the given SOP function, we have one compliment term, B. So, to represent the compliment input, we are using the NOT gates at the input side. And to represent the product term, we use AND gates. See the below given logic diagram for representation of the Boolean function.
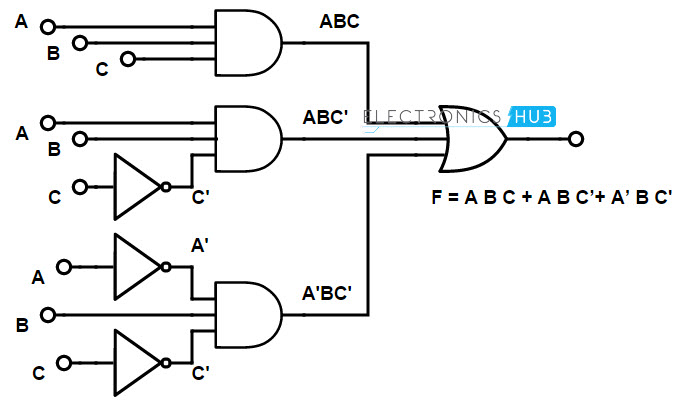
Implementation for 3 Input Variables
Let us now see how to implement the following Boolean function by using basic logic gates. It is a 3 input variable function.
F = A B C + A B C + A B C
In the given function, we have two compliment terms, A and C. So, to represent the compliment input, we are using the NOT gates at the input side. And to represent the product term, we use AND gates. See the below given logic diagram for representation of the Boolean function.
POS Boolean Function Implementation using Logic Gates
The product of sums or POS form can be represented by using basic logic gates like AND gate and OR gates. The POS form implementation will have the OR gate at its input side and as the output of the function is product of all sum terms, it has AND gate at its output side. In POS form implementation, we use NOT gate to represent the inverse or complement of the variables.
| Product of Sums (POS) | |
| Input | OR |
| Output | AND |
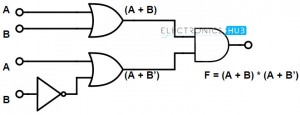
Implementation for 2 Input Variables
Let us now see how to implement the following Boolean function by using basic logic gates.
F = (A + B) . (A + B)
In the given function, we have a complement term, B. So, to represent the compliment input, we are using the NOT gates at the input side. And to represent the sum term, we use OR gates. See the below logic diagram for representation of the Boolean function.
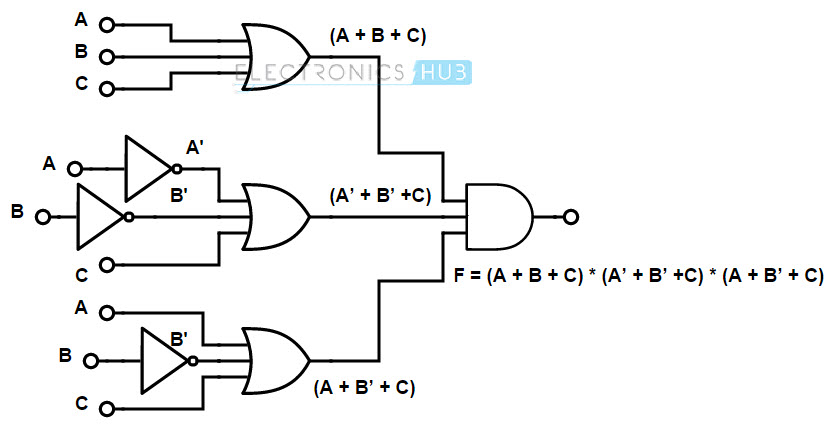
Implementation for 3 Input Variables
Implement the Boolean function by using basic logic gates.
F = (A + B + C) . (A + B +C) . (A + B + C)
In the given Boolean Function, we have two compliment terms, A and B. So, to represent the compliment input, we are using the NOT gates at the input side. And to represent the sum term, we use OR gates. See the below given logic diagram for representation of the Boolean function.
Implementation of Boolean functions using Universal Logic Gates
NAND gate and NOR gate are considered to be ‘Universal Logic Gates’. The reason behind this is, NAND gate and NOR gate can perform (or can function like) all the 3 basic gates, such as AND gate, OR gate and NOT gate. We can design any basic logic gate by using NAND gate or NOR gate. This is why they are called as “Universal Gates”.
Let us see the implementation of the Boolean functions using universal logic gates.
Implementation of Boolean functions using NAND gates
NAND gate is a logical combination of AND gate and NOT gate and this can function like AND gate, OR gate and NOT gate. So, we use NAND gates to implement the Boolean function.
The important thing to remember about NAND gate is this is the inverse of basic AND gate. This means the output of the NAND gate is equal to the complement of the output of the AND gate.
Let’s see an example to understand the implementation.
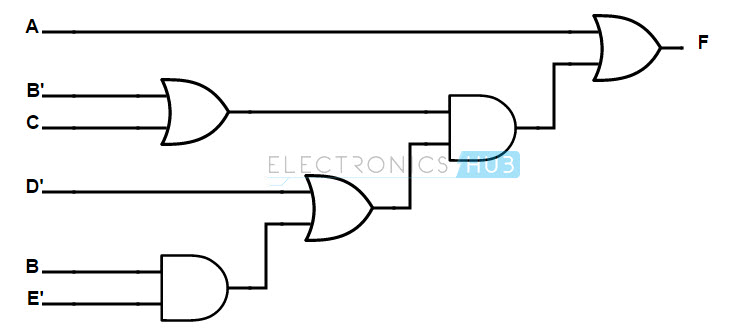
Implement the Boolean function by using a NAND logic gate.
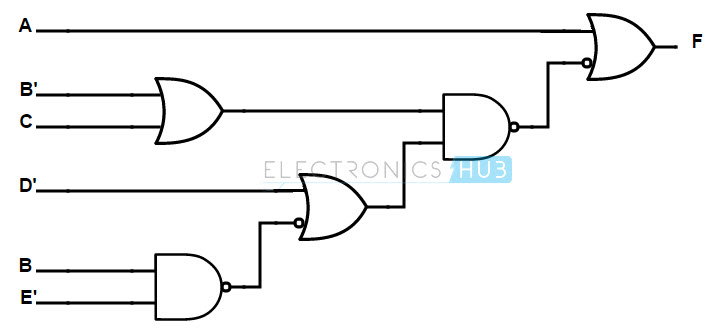
F (A, B, C, D, E) = A + (B + C) (D + BE)
In NAND gate implementation, we use NAND gates at both input and output side. Observe the designed logic diagram below. The step by step procedure to implement the given Boolean function using NAND gates is shown below.
First, the given Boolean function or equation should be represented using AND-OR gates. The AND-OR implementation is shown below.
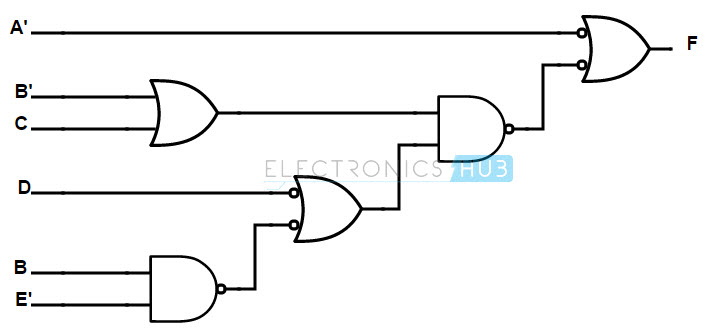
In order to convert the AND gates into NAND gates, a bubble (complement) is introduced at the output of the AND gate. To compensate the bubble, the input of the next gate is also introduced with a bubble. The implementation is shown below.
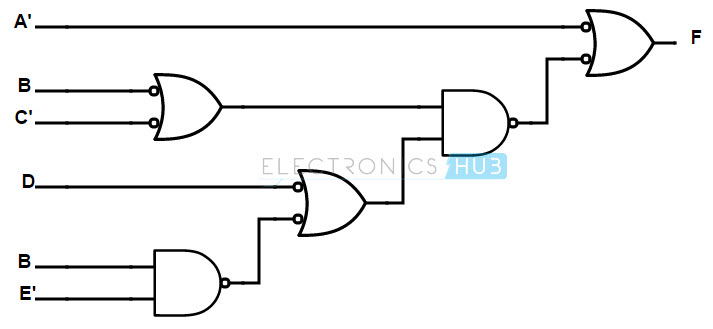
To impose uniformity at the input, if a gate has one input with a bubble, the other input is also introduced with a bubble. Again, in order to compensate the bubble, the output of the preceding gate is introduced with bubble or complement the literal. The same is shown in the following figure.
If an OR gate is not having any bubble at either of the inputs, bubbles are introduced and are appropriately compensated as shown in the figure below.
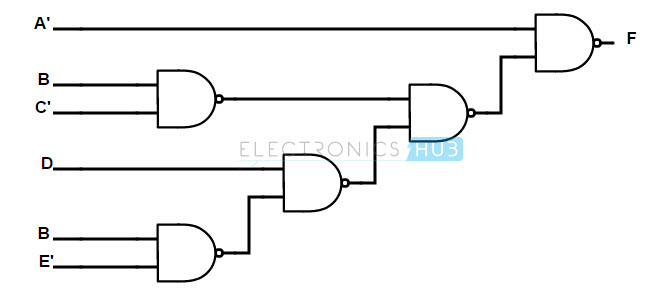
An OR gate with two complemented inputs is equivalent to a NAND gate (according to DeMorgan’s Law A’+B’ = (AB)’). Hence, replacing the OR gate, which is having two complemented inputs, with NAND gate, we get the final structure of the implementation of the Boolean function using NAND gates. The final implementation is shown below.
Implementation of Boolean functions using NOR gates
NOR gate is the combination of OR gate and NOT gate and this can function like AND gate, OR gate and NOT gate. So, we use NOR gate to implement the Boolean functions. The important thing to remember about NOR gate is it is the inverse of basic OR gate. This means the output of the NOR gate is equal to the complement of the output of the OR gate.
Let’s see an example to understand the implementation.
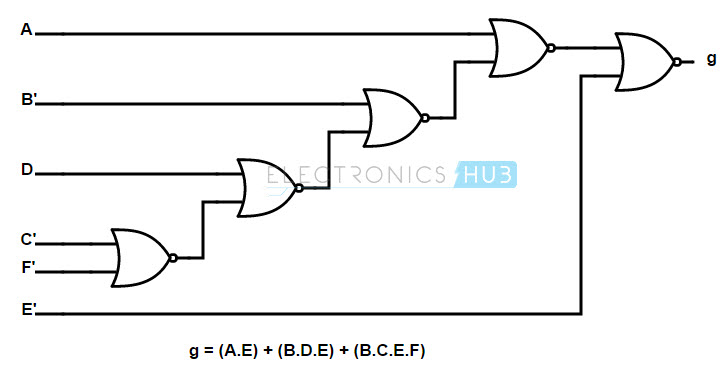
Implement the Boolean function by using NOR logic gate.
g (A, B, C, D, E, F) = (A E) + (B D E) + (B C E F)
We can rewrite the given equation as:
g (A, B, C, D, E, F) = A E + B D E + B C E F
= (A + B D + B C F) E
= (A + B (D + C F)) E
In NOR gate implementation, we use NOR gates at both input and output side. Observe the designed logic diagram below.

Conclusion
A complete beginner’s tutorial on Implementing Boolean Functions using Logic Gates. You learned some basics of logic gates (AND, OR, NOT), Sum of Products (SOP) and Product of Sums (POS) representation of equations and their implementation using logic gates and also implementation of Boolean expressions using Universal Gates (NAND and NOR).


7 Responses
Very useful
Can you solve this using nor gate ONLY-
B'(CD)’+A’C’D
s.o.p expression is best suited with nand gate only.
I want to enquire how to implement the A/B using logic gates
Can u solve this boolean expression using nand gate f=A(B+CD)+BC’
this is great
Pls can you solve this using nand gate F=X’Y’Z+X’YZ+XY’
And also pls give the required truth table xxxx