In general, we represent the positive (unsigned) numbers without any sign indication and negative numbers with ‘minus’ (negative sign) sign before them. But these are not applicable for computing in the digital systems like, computers , as the data is represented in binary number system. So to represent the sign a special notation is required.
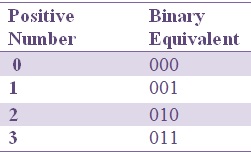
Positive Signed Binary Numbers
The binary numbers having their MSB 0 are called “Positive signed binary numbers”.
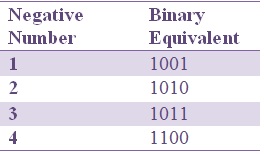
Negative Signed binary numbers
The binary numbers having their MSB 1 are called “Negative signed binary numbers”.
Unsigned numbers can have a wide range of representation. But whereas, in case of signed numbers, we can represent their range only from – (2(n-1) – 1) to + (2(n-1) – 1).
Where n is the number of bits (including sign bit).
Ex: For a 5 bit signed binary number (including 4 magnitude bits & 1 sign bit), the range will be
– (2(5-1) – 1) to + (2(5-1) – 1)
-(2(4) – 1 ) to + (2(4) – 1)
-15 to +15
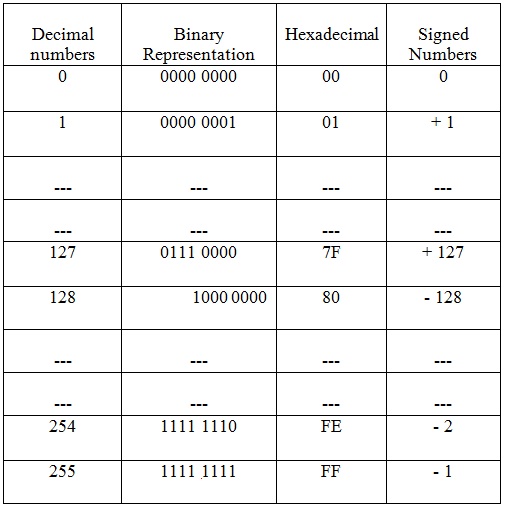
Unsigned 8- bit binary numbers will have range from 0-255. The 8 – bit signed binary number will have maximum and minimum values as shown below.
The maximum positive number is 0111 1111 +127
The maximum negative number is 1000 0000 -127
As we cannot feed positive or negative signs to the digital system, these should be represented in some other ways. There are three common ways to represent negative numbers within the computer. They are
- Signed magnitude representation.
- 1’s compliment representation.
- 2’s complement representation.
Signed magnitude representation
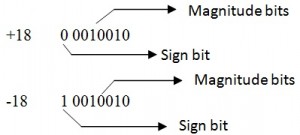
The binary numbers which can be identified by their MSB (Most Significant Bit), whether they are positive or negative are called “Signed binary numbers”.
Ex: 1001 — > + 9 (positive) 1 001 — > – 1 (negative)
This is the simplest way of representing the both positive and negative numbers in binary system. In the signed magnitude representation,
- Positive number is represented with ‘0’ at its most significant bit (MSB).
- Negative number is represented with ‘1’ at its most significant bit (MSB).
One’s Complement of a Signed Binary Number
1’s complement is another way of feeding the negative binary number to the computer. In one’s complement method , the positive binary numbers are unchanged. But the negative numbers are represented by taking 1’s complement of unsigned positive number.
A positive number always starts with 0, at its MSB while a negative number always starts with 1, at its MSB.
1’s compliment of a number is created by replacing all 0’s with 1’s & all 1’s with 0’s.
For example, if a binary number is 01101001, then its one’s complement is 10010110.
Let’s see some more examples about 1’s complement.
Ex 1: -33 =?
33 is represented as (100001)2
In 8 bit notation, it is represented as (0010 0001)2
Now, -33 is represented in one’s compliment as (1101 1110)2
Ex 2: -127 =?
In 8 bit notation, 127 is represented as (0111 1111)2
Now, -127 is represented in one’s compliment as (1000 0000)2
Ex 3: -1 =?
1 is represented as (001)2
In 8 bit notation, it is represented as (0000 0001)2
Now, -1 is represented in one’s compliment as (1111 1110)2
1’s Complement Using Inverters
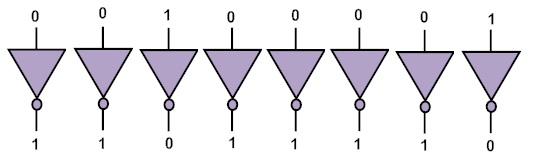
The simplest way of finding the 1’s complement of a required number, for digital electronic circuit is to make use of “Inverters”. As the name implies, an inverter is the device / circuit which generates the compliment of its input.
The inverters are connected in parallel to get the 1’s compliment of its input binary number. No matter if a binary number has any number of digits, we can easily find its one’s complement. Just by writing all 0’s as 1’s & 1’s as 0’s will give the 1’s compliment of a binary number.
The mathematical operations performed on binary numbers is called “Binary Arithmetic”. We can add or subtract any positive or negative number in many ways like, A + B, A + (-B), -B + A etc.
Addition of Signed Binary Numbers
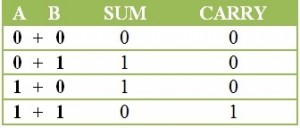
Binary addition also follows the same rules as normal addition. But here, the only exception is that the mathematical operation will be performed between only two digits (0 & 1); and always 1 > 0.
Rules for binary Addition
Subtraction using 1’s compliment
To subtract a number from another binary number, first it has to be converted into its one’s compliment.
There are 3 possible cases for subtracting the negatives numbers by using 1’s compliment.
Case 1 : Negative number smaller than positive number.
Ex: (28)10 & (-15)10
We know 28 is represented in binary number system as (011100)2
15 is represented in binary number system as (01111)2
1’s compliment of 15 is (10000)2 i.e. -15
(13)10 is same as 0 01101 in binary system.
Case 2: Negative number greater than positive number.
Ex: (-28)10 & (15)10
We know 28 is represented in binary number system as (011100)2
15 is represented in binary number system as (01111)2
1’s compliment of 28 is (100011)2 i.e. -28
(-13)10 is same as 1 10010 in binary system.
Case 3: both are negative.
Ex: (-28)10 & (-15)10
We know 28 is represented in binary number system as (011100)2
1’s compliment of 28 is (100011)2i.e. -28
15 is represented in binary number system as (01111)2
1’s compliment of 15 is (10000)2 i.e. -15
(-43)10 is same as 1010100 in binary system.
Two’s Complement of a Signed Binary Number
The process of finding is similar to the process of calculating 10’s compliment of decimal numbers. To find the 2’s compliment of a binary number, first we should find the 1’s compliment of that number and later “1” is added to the 1’s compliment.
Two’s compliment representation of positive numbers is same as the representation of 1’s Compliment and signed magnitude representation.
Finding the 2’s compliment involves in two steps stated below,
Step 1: find the one’s compliment
Step 2: add ‘1” to the unsigned number result.
Let’s understand this by some examples.
Ex 1: -33 =?
33 is represented as (100001)2
In 8 bit notation, it is represented as (0010 0001)2
Now, -33 is represented in one’s compliment as (1101 1110)2
Adding 1 (0000 0001) to it,
The result is (1101 1111)2
Therefore, the two’s complement of the number – 33 is (1101 1111)2.
Ex 2: -127 =?
In 8 bit notation, 127 is represented as (0111 1111)2
Now, -127 is represented in one’s compliment as (1000 0000)2
Adding 1 (0000 0001) to it,
The result is (1000 0001)2
Therefore, the two’s complement of the number -127 is (1000 0001)2
Ex 3: -1 =?
1 is represented as (001)2
In 8 bit notation, it is represented as (0000 0001)2
Now, -1 is represented in one’s compliment as (1111 1110)2
Adding 1 (0000 0001) to it,
The result is (0000 0010)2
Therefore, the two’s complement of the number -1 is (0000 0010)2
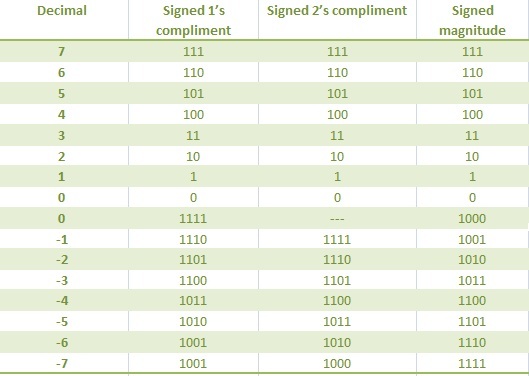
TABLE REPRESENTING 1’S & 2’S COMPLEMENTS OF DECIMAL NUMBERS
SIGNED BINARY NUMBERS SUMMARY
The binary numbers which can be identified by their MSB are called “Signed binary numbers”.
If MSB is 1, they are “Negative signed binary numbers”. Ex: – 1 = 1001
If MSB is 0, they are “Positive signed binary numbers”. Ex: + 9 = 1001
Computers cannot understand minus symbol. So to give the negative numbers as their inputs we will follow 3 special methods. They are
1) Signed magnitude representation
2) 1’s compliment representation
3) 2’s compliment representation
1’s compliment means “Replacing all 1’s with 0’s & 0’s with 1’s”.
Ex: 1’s compliment of 15, which is equal to – 15 is (10000)2 i.e. -15
2’s compliment means “Adding 1 to the 1’s compliment of the required number”.
Ex: 2’s compliment of the number – 33 is (1101 1111)2.
The mathematical operations like addition and subtraction of binary numbers is called “Binary Arithmetic Operations”.

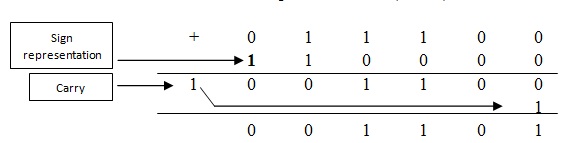
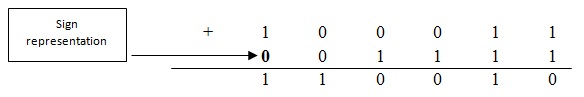
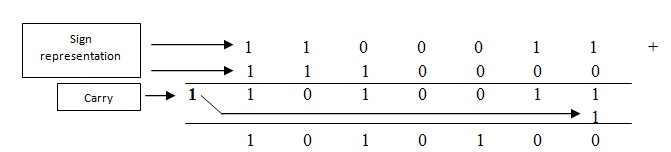

4 Responses
A simple, useful and easily understandable note.
simple easy and conceptual notes
Easy To Understand!!!!
The example Ex 3: -1 =? in two’s compliment is wrong:
1 is represented as (001)2
In 8 bit notation, it is represented as (0000 0001)2
Now, -1 is represented in one’s compliment as (1111 1110)2
Adding 1 (0000 0001) to it,
—>>>>>>> The result is NOT (0000 0010)2 but (1111 1111).