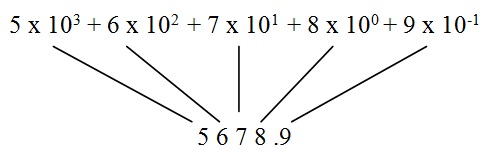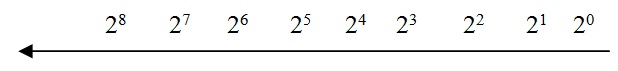Converting binary to decimal involves understanding the value each binary digit (bit) represents in the decimal system. Each bit is assigned a power of 2, based on its position from right to left, starting with 20.
For example, to convert the binary number 1011 to decimal:
- Multiply each bit by its corresponding power of 2: (1×23) + (0×22) + (1×21) + (1×20)
- Sum the results: 8 + 0 + 2 + 1 = 11
- The decimal equivalent of binary 1011 is 11.
Outline
ToggleDecimal Number System Overview
This is the number system which we are using in our daily life. In this system, we consider the positions of digits in a number as units, tens, hundreds, thousands & etc. The position of a digit with reference to the decimal point determines its value. The base of the decimal number is 10. Let us calculate a number in decimal system as follows.
Ex:
848: Eight hundred and forty eight. It is 800 + 40 + 8
8 hundred = 8 x 100 = 8 x 102
4 tens = 4 x 10 = 4 x 101
8 units = 8 x 1 = 8 x 100
Now, 8 x 102 + 4 x 101 + 8 x 100 = 848
Here the left most bit is called “Most significant bit” or “MSB” and the right most bit is called “Least significant bit” or “LSB”.
Let’s see another example:
5678.9 It is 5000 + 600 + 70 + 8 + 0.9
In power of 10 we can write the above number as
5 x 103 + 6 x 102 + 7 x 101 + 8 x 100 + 9 x 10-1
5 6 7 8 .9
Binary Number System Overview
The binary number system uses only two digits 0 & 1. It is a positional number system this means the positions are weighted as the powers of 2. Mostly binary system is used in digital systems. The data to the computer , must be in the form of binary digits 0’s & 1’s.
Examples for understanding the binary number system
21 is expressed in binary system as 101012 = 1 × 24 + 0 × 23 + 1 × 22 + 0 ×21 + 1 ×20 = 16 + 4 + 1 = 21
23 is expressed in binary system as 101112 = 1 × 24 + 0 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 16 + 4 + 2 + 1 = 23
35 is expressed in binary system as 1000112 = 1 × 25 + 0 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 1 × 20 = 32 + 2 + 1 = 35
0 or 1 is called as ‘BIT’.‘NIBBLE’ is a combination of 4 bits. ‘BYTE’ is a combination of 8 bits. In general we will measure the size of memory in Bytes.
Binary To Decimal Conversion
We can convert a binary number to decimal number by 2 ways. They are
1.Multiplying Each Binary Number by its Position Value
Counting from right, the value of the right most bit is 1 , value of next bit is 2 , value of next bit is 4 and value of next bit is 8 and so on.
For example, convert 1011 to decimal number
Sol
8 x 1 + 4 x 0 + 2 x 1 + 1 x 1 = (11)10
(8) (0) (2) (1)
2.Repeated division by 2
A well known and easy method for converting decimal numbers into binary numbers is “Repeated division by 2”.
The method of converting whole numbers from one base to another is known as “Repeated division”. When the decimal number is divided with its base number, we get a quotient called “Reminder”. The reminder is recorded as first binary digit and the quotient is again divided by the base number, thus we get second quotient and second reminder. This is recorded as second binary digit and this process will go on till the quotient becomes 0.
In this way, if a decimal number is divided by 2 then the reminder is only 0 or 1. The binary result is obtained by writing the first reminder as ‘Least significant bit’ and the last reminder as ‘Most significant bit’.
Let’s try this with an example: odd number
43 ÷ 2 Quotient 21, remainder 1 Result > 1
21 ÷ 2 Quotient 10, remainder 1 Result > 1 1
10 ÷ 2 Quotient 5, remainder 0 Result > 0 1 1
5 ÷ 2 Quotient 2, remainder 1 Result > 1 0 1 1
2 ÷ 2 Quotient 1, remainder 0 Result > 0 1 0 1 1
1 ÷ 2 Quotient 0, remainder 1 Result > 1 0 1 0 1 1
Even number
36 ÷ 2 Quotient 18, remainder 0 Result > 0
18 ÷ 2 Quotient 9, remainder 0 Result > 0 0
9 ÷ 2 Quotient 4, remainder 1 Result > 1 0 0
4 ÷ 2 Quotient 2, remainder 0 Result > 0 1 0 0
2 ÷ 2 Quotient 1, remainder 0 Result > 0 0 1 0 0
1 ÷ 2 Quotient 0, remainder 1 Result > 1 0 0 1 0 0
Another example
convert 9310 to binary
93 / 2 = 46 remainder 1 (least significant digit)
46 / 2 = 23 remainder 0
23 / 2 = 11 remainder 1
11 / 2 = 5 remainder 1
5 / 2 = 2 remainder 1
2 / 2 = 1 remainder 0
1 / 2 = 0 remainder 1 (most significant digit)
The binary representation of (93)10 is 1 0 1 1 1 0 1.
If we divide an even decimal number by 2, then we get reminder as 0. If we divide an odd decimal number we get reminder as 1.
The binary result of a decimal number can be obtained by arranging the first reminder at MSB and last reminder at LSB.
Representation of a Binary Number
We already know that the decimal system is represented with base 10 this means that the weight of each digit (starting from left) increases by a factor of 10. Similarly, all binary numbers are represented with base 2 so that the weight of each digit (starting from left) increases by a factor of 2 i.e. the first digit is stated as 20 and second digit as 21 and so on.
As we learned in binary number system in previous session, the least possible power of 2 is 20 and highest is 28 (in 8- bit binary system).
To understand this clearly, see the below figure.
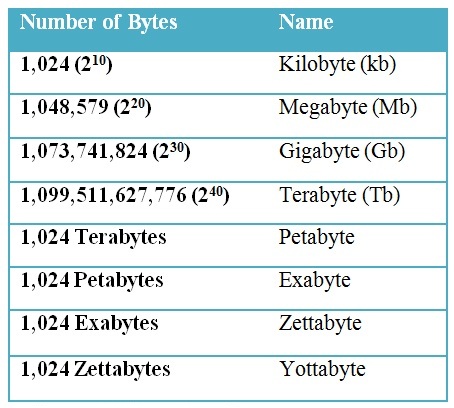
Binary Number Names and Prefixes
Number Names
Binary numbers also perform mathematical operations like addition and subtraction. So in addition and subtractions the decimal numbers are represented as a group of binary digits (0 & 1). Basically, group of binary digits are known in 3 forms. They are Bit, Byte and Word.
0 or 1 is called ‘Bit’
4 bits are called ‘Nibble’
8 bits or 2 nibbles are called as ‘Byte’
16 bits or 4 nibbles or 2 bytes are called as ‘Word’
32 bits or 8 nibbles or 4 bytes or 2 words are called ‘Double’
64 bits or 16 nibbles or 8 bytes or 4 words or 2 doubles are called ‘Quad’
Number Prefixs
While we are converting the data / information in digital systems from one notation to another i.e. from binary to decimal & decimal to binary; we should follow only one of the either notations, why because the data may vary from one notation to another. For example, if we are saying “Ten”, we will represent it as “10” in decimal & it may seems like “1” and “0” (which is equal to the number 2) in binary notation.
We can overcome this problem by writing a subscript at the end of the number or digits. This subscript is called “prefix”. For example, if we are representing the numbers in binary system, we have to represent as (1101011)2 & for decimal number system as (432)10 & for Hexa decimal number system representation as (480)hex.
Now – a – days the digital electronic world has been developing rapidly and the representation of numbers has a new way. They have a huge range from bit (smallest) to yottabyte (largest).
Summary
In general, we use Terabyte as highest size of memory measurement.
- The word “Binary Digit” is called “BIT”.
- Decimal system is that we use to represent numbers, regularly.
- In decimal system, the numbers are represented with base 10. Ex: (432)10
- Binary numeric system or Binary number system has only two digits (0 and 1)
- The binary numbers are weighted from left to right as a power of 2.
- There are two ways to convert a decimal number into binary number.
- Sum of weights method.
- Repeated division by 2.
- While converting the numbers from binary to decimal or decimal to binary, we will follow a prefix notation to avoid the occurrence of errors in understanding the type of numeric system in which we are representing the number.
- Binary numbers are represented in many names like Bit, Nibble, Byte, Word etc. In which Bit is the smallest and Terabyte is highest.
In further tutorials we are going to study about octal and Hexa decimal number system and their conversions.