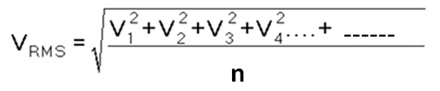The Alternating current changes its direction periodically. It is time dependent. We can explain and understand the characteristics by plotting the instantaneous values of the AC current. This wave form plot is named as ‘AC wave form’. To measure the different parameters of AC wave form there are different methods . All these are explained it his tutorial.
Outline
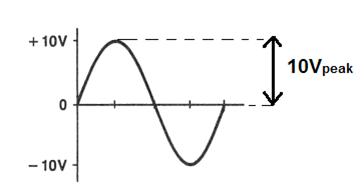
TogglePeak Value Of an AC Waveform
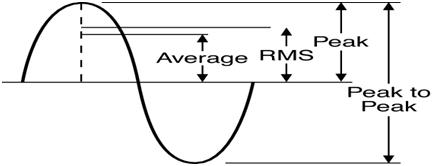
The maximum value of a positive half cycle or a negative half cycle is called as “Peak value”. It is represented by Im. It is the maximum voltage attained by the AC wave.
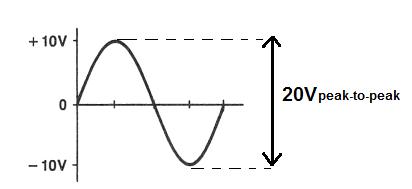
Peak – to – Peak Value
“Peak – to – peak” voltage is the voltage measured between the maximum positive and negative amplitudes of a sine wave. It is double that of amplitude of the AC wave form. This is the maximum voltage value of the wave form.
It is denoted by VPK.
Average Value
This is the average of all values of a half cycle of an AC wave. To find the average value of an alternating wave form, one half cycle is divided in to equally spaced ordinate. By calculating the average voltage of these instantaneous voltage values we get the average value of AC wave form. It is the quotient of the area under the waveform with respect to time.
The Average value is 0.637 times to the peak to peak value.
VAV = VPK x 0.637
We can calculate the average value by the below given formula.
VAV=(Sum of all mid-ordinates)/(Number of mid-ordiantes)
VAV = V1 + V2 + V3 + – – – – – – + Vn / n
RMS Voltage
This stands for Root Mean Square and it is the standard way of measuring and reporting alternating current and voltage. The RMS can be calculated by multiplying the peak to peak voltage by the square root of 2 (approximately 0.707).
VRMS = VPK x 0.707
RMS value is defined as the “Square root of the averages of the squares of all voltages in the wave form”.
RMS value is the most commonly used method to represent the voltage of an Ac wave form.
The RMS value can be represented in the form of other voltages,
VRMS = Vpeak x 1 / 2
VRMS = Vpeak to peak x 1 / 22
VRMS = Vavg x π / 22
Importance of RMS value
In case of alternating currents, the magnitudes of the current are expressed in the form of RMS values.
In general, we used to say that the house hold current is of 120 Volts AC,. This actually means, the RMS voltage of house hold power is 120 V.
The heat produced in the coil, because of the flow of alternating current is proportional to the square of the RMS value of the current.
We can measure the RMS voltage with all voltmeters. In some expensive voltmeters, first the peak voltage is calculated and then multiplying it by 0.707, we get the RMS voltage value, most accurately.
Form factor and Crest factor
Form Factor
“The Form factor is the ratio of RMS voltage value of an alternating wave to its average voltage”.This is represented by Kf.
Form factor = RMS voltage / average voltage
Kf = Vrms / Vavg
By the relation between average voltage value and RMS value, we can calculate the form factor as
Kf = 0.707 Vmax / 0.637 Vmax
= 1.11
Crest Factor
“The Crest factor is the ratio of peak voltage value to its RMS voltage value”. The crest factor is also known as “Peak factor” & “Amplitude factor”.
This is represented by Kp.
Form factor = Peak voltage / RMS voltage
Kp = Vpeak / Vrms
By the relation between peak value and RMS value, we can calculate the Crest factor as
Kp = Vmax / 0.707 Vmax
= 1.414
Example
Find out all the AC measurements of a wave with 10 V amplitude and 20 Hz frequency and average value of 6.3v.
Sol:
Given, peak value is 10
Peak to peak voltage is = 2 x peak voltage
= 2 x 10
= 20 Volts
Time period = 1 / f
= 1 / 20
= 0.05 sec
RMS voltage value = Vpeak x 0.707
= 10 x 0.707
= 7.07 V
Angular velocity (ω) = 2π f (rad/s)
= 2 x 3.1416 x 20
= 125.6 rad/sec
Form factor Kf = Vrms / Vavg
= 7.07 / 6.3
= 1.11
Crest factor Kp = Vpeak / Vrms
= Vmax / 0.707 Vmax
= 10 / (0.707 x 10)
= 1.414
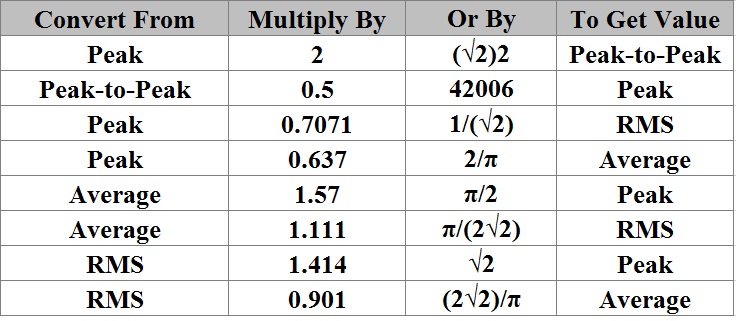
Measurements Conversion Table
By using form factor and crest factor, by using RMS value and average values of waves we can find out shape of a waveform. But sometimes we will get confused while we convert various sinusoidal waveforms. The table provided below will help us to convert one sinusoidal wave values to another.
Relationship Between Frequency and Periodic Time
The frequency of a wave form is defined as “The number of cycles per second”. This means the number of complete oscillations performed by an alternating wave, in one second”.
Frequency (f) = 1 / Time period
Units are Hertz.
As the time period and frequency are reciprocal to each other, we can define the time period as “The inverse of frequency”.
Time period (t) = 1 / frequency
Units are seconds and milliseconds.
Some standard conversions between frequency and time
- 1 KHz (Kilohertz) = 1 ms (milliseconds)
- 1 MHz (Megahertz) = 1 us (microseconds)
- 1 GHz (Gigahertz) = 1 ns (nanoseconds)
- 1 THz (Terahertz) = 1 ps (picoseconds)
Example
Calculate periodic time of AC signal whose frequency is 60Hz?
Sol: Periodic time of the AC signal is T = 1/f
Given that frequency of signal f = 60 Hz
Time period (T) = 1/f
= 1/60 sec
= 0.01666 sec
= 16.66 ms (milliseconds)
The time period of the wave form is 16.66 ms.