Among all the waveforms , sine waves are frequently used because of their ease of representation and some specific advantageous characteristics. The sine or sinusoidal wave is a curve that describes a smooth repetitive oscillation.
We can define the sine wave as “The wave form in which the amplitude is always proportional to sine of its displacement angle at every point of time”.
Outline
ToggleWhat Is A Sinusoidal Waveform?
A Sinusoidal Waveform is shaped like a sine wave used in alternating current (AC) circuits. It is a repeating curve oscillates between positive and negative values that represents the variation of voltage over time.
All waves can be made by adding up sine waveforms. The sine wave has repetitive pattern. The length of this repeating piece of the sine waveform is called the wavelength.
Characteristics of a Sine Wave are:
- Amplitude: The maximum value of the waveform, measured from the zero line to the peak.
- Period: The time it takes for one complete cycle of the wave.
- Frequency: The number of cycles per second, measured in Hertz (Hz).
- Phase: The position of the waveform relative to a reference point.
Sinusoidal Waveform Equation:
It’s most basic form as a function of time (t) is
Y(t)= A sin(2πft+ φ)=A sin(ωt+ φ)
Where
A is the amplitude,
F is the frequency,
ω = 2πf, angular frequency,
φ is phase
A sine wave look like as below:
Generation Of Sine Waveform
There are many methods to generate sinusoidal waveform. They are listed below.
- Quartz Crystal Oscillator
- Negative Resistance Oscillator
- Basic Single Coil AC Generator
- Phase Shift Oscillator
- Wein Bridge Oscillator etc.
The basic method for generating sine wave is “ Basic single coil generator” which is already explained in our previous article “AC theory”.
What is R.P.M.?
R.P.M. Stands for “Revolution per Minute”. This means ‘The number of revolutions made by a coil’ is called “RPM”. For suppose a shaft of a motor is completing 100 revolutions in a minute, then the speed of the motor is said to be ‘100 RPM’
The number of poles is always an even number.
The relation between the RPM of the coil, the frequency of the produced sine wave and the number of poles is given below.
Generally we say ω = 2πf, but in case of rotation takes place because of magnetic poles, we write the angular velocity as
ω = (2 / n) [2πf] where n represents the no of poles
As we know n = 60 f, then
Number of revolutions can be written as,
N p =(2×60)f/p
ωrotor=(2/Poles) x 2 πf(rad/sec)
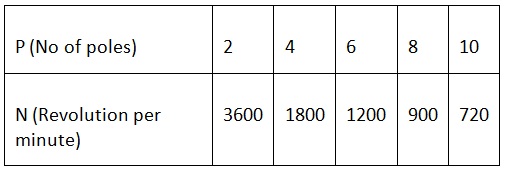
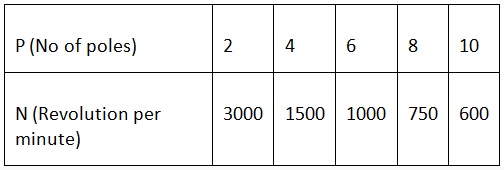
Np=120f/Poles (RPM)
Where
ω is the angular velocity of the sine wave
N is the number of poles.
F is the frequency of the wave form.
π Is a constant with a value of 3.1416.
The number of poles vs speed of a 60 Hz frequency machine is
The number of poles vs speed of a 50 Hz frequency machine is
Instantaneous Voltage
Instantaneous voltage is the voltage between two points at a particular moment in time. The voltage of a waveform at a given instant in time is called “Instantaneous voltage”.
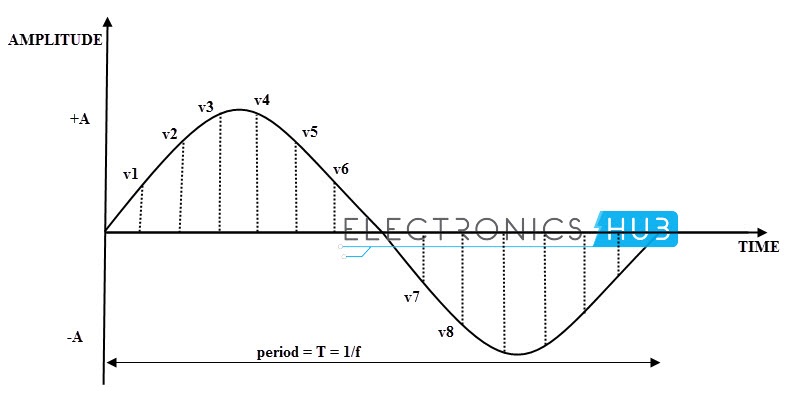
In the above diagram v1, v2, v3, v4, v5, v6…… are the instantaneous voltages of the sine wave.
To find the instantaneous voltage value of the sine wave, we depend on Maximum voltage of the sine wave.
Instantaneous voltage = Maximum voltage x sin θ
Vinst = Vmax x sin θ
Displacement of a Coil With in a Magnetic Field
The displacement of the sine wave is found by the angle of rotation of the coil. It is represented by ‘θ’. In fact, to find the instantaneous voltage we multiply the maximum or peak to peak voltage of the sine wave with the sine of the coil rotation angle.
Angle of rotation of coil in a magnetic field is θ = ωt
Where
ω is the angular velocity of the sine wave
t is the time period of the sine wave.
For a known value of a maximum voltage of the sine wave, we can calculate the instantaneous voltages along the waveform. As the instantaneous value gives the positional value of the sine wave we can plot the graph on the sine wave. This gives the shape of the sine wave.
The above picture shows the amplitude of the sine wave. In fig (1) the armature in the magnetic field is moving at high amplitude, so the generated sine wave will form positive half cycle. But in fig (2) the armature in the magnetic field is moving at low amplitude, so the generated sine wave will form negative half cycle.
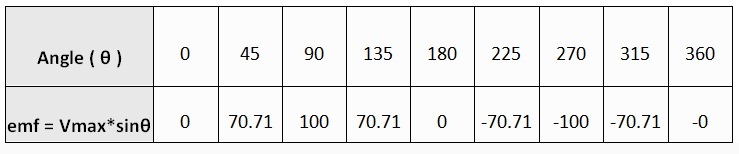
To understand this easily, we will plot the instantaneous values of sine wave at every 45o. In one complete cycle, we can have 8 values for every 45o of angle.
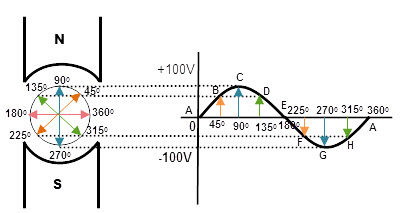
Sinusoidal Wave Construction
By plotting the graph at different instances of the rotating coil in the magnetic field, from 0o to 360o we can draw the sine wave pattern. In that, when the sine wave phase is 00, 1800 and 360 0, the amplitude of the sine wave is 0 that means there is no EMF induced in the rotating coil.
This is because, no part of the moving coil is affected by magnetic flux lines. The zero EMF induced at the positions A & E. Similarly, at 900 and 2700 of phase, the sine wave will have the maximum amplitude. It occurs at C & G.
At other positions of the sine wave (B, D, F, H) the EMF will be as per the formula, e = Vmax*sinθ.
The EMF value of the sine wave with respect to the phase angle of the moving coil is given below.
So the sine wave has high amplitude (positive) at 900 and high amplitude value (negative) at 2700.
Angular Velocity of Sine Wave
This is the rate of change of angular displacement with respect to time. “Angular velocity” is a measurement of the rate of change of angular position of an object over a period of time. It is denoted by ω.
It is a vector quantity. Units for Angular velocity: RADIANS or degrees
ω = 2π f (rad/s)
As the frequency of AC current in India is 50 Hz, the angular velocity can be measured as 314.16 rad / sec.
Angular velocity is defined as the velocity of the circular motion of the coil in AC current generator.
As we already explained above, it is denoted by ω. It is a function of the time period of the sine wave, i.e. the time taken to complete one revolution (T).
We know that the frequency is inversely proportional to the time period of the sine wave. i.e. f = 1 / T. By this, the angular velocity of the sine wave in Time period is given as
ω=2 π / T (rad/s)
From the above equation, we can say that, the angular velocity of the sine wave is inversely proportional to the time period of the sine wave. That means for higher the value of time period, the lower is the angular velocity and vice versa.
Sinusoidal Waveform Example
If a sine wave is defined as Vm¬ = 150 sin (220t), then find its RMS velocity and frequency and instantaneous velocity of the waveform after a 5 ms of time.
Solution:
The general equation for the sine wave is Vt = Vm sin (ωt)
Comparing this to the given equation Vm¬ = 150 sin (220t),
The peak voltage of the maximum voltage is 150 volts and
Angular frequency is 220 rad / sec.
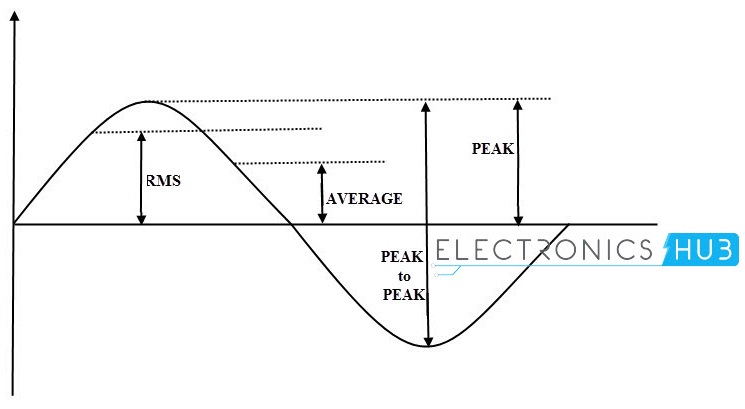
The RMS velocity of the wave form is given as
Vrms = 0.707 x max amplitude or peak value.
= 0.0707 x 150 = 106.05 volts
The angle of a sine wave is a function of its frequency, as we know the sine wave’s angular velocity, so we can find out the frequency of the waveform. By using the relation between ω and f
Angular velocity (ω) =
Frequency (f) = ω / 2 π
For the given sine wave form ω = 220,
Frequency = 220 / 2 π
= 220 / ( 2 x 3.1416)
= 220 / 6.2832
= 35.0140 Hz
The instantaneous value is given by after a time of 5 ms can be calculated by using the below formula.
Vi = 150 sin (220 x 5 ms)
= 150 sin (1.1)
= 150 x 0.019
= 133.68 volts
Phase of the angle at time t = 5 ms are calculated in radians. We can convert the radian values into degree values very simply. The formula for conversion of radians to degrees is
Degrees = (1800/ π)×radians
Converting 1.1 radians into degrees,
= (1800 / π) x 1.1
= 63.02 degrees
AC Circuits and Sine Waves
Sine waves are the fundamental waveform used in AC circuits. When a sinusoidal voltage is applied to a circuit, it causes a sinusoidal current to flow. The relationship between the voltage and current depends on the components in the circuit (resistors, capacitors, inductors).
The behavior of sine waves in AC circuits depends on the below components:
Resistors: In a purely resistive circuit, the current and voltage are in phase.
Capacitors: In a purely capacitive circuit, the current leads the voltage by 90 degrees.
Inductors: In a purely inductive circuit, the current lags the voltage by 90 degrees.
Conclusion:
sinusoidal waveforms are the cornerstone of AC circuits. Their properties, including amplitude, period, frequency, and phase, are fundamental to understanding the behavior of electrical components in alternating current systems. The interplay between voltage and current, characterized by phase relationships, significantly impacts circuit performance. By grasping these concepts, engineers and technicians can effectively analyze, design, and troubleshoot AC circuits, optimizing power delivery and system efficiency.
A deep understanding of sinusoidal waveforms and their interactions within AC circuits is essential for various applications, from power generation and transmission to electronics and communication systems.



4 Responses
What is rms
Root mean square.
The way to work out RMS is multiplying the peak of the wave by 0.707
I am not a company. I have been told to download a graded sine wave to help determine the frequency range of some speakers I have. I would appreciate it if you could help me find where I can download one?
There is a website called “https://onlinetonegenerator.com/”. You can use this site to generate different waveforms (including sine) at your specified frequency. There is also a subwoofer testing option in the site. I don’t know whether you can download the waveforms or not but it is a start.