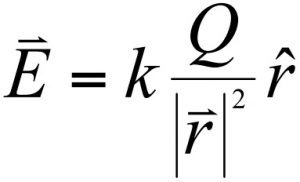In this tutorial, we will learn about two important concepts in Electrostatics i.e. Electric Flux and Gauss’s Law. This tutorial explains the concepts of Electric Flux, Flux Lines, Gauss’s Law, its statement and its applications.
There is already a tutorial on Electrostatics. Visit ‘”ELECTROSTATICS” for more information.
Outline
ToggleIntroduction
Before going further into the main topics of discussion, let us quickly recap some of the important concepts. Electric Field is defined as the force per unit charge at a particular point.
E = F / q
For example, the Electric Field of a point charge ‘Q’ on a test charge ‘q’ at a distance is given by
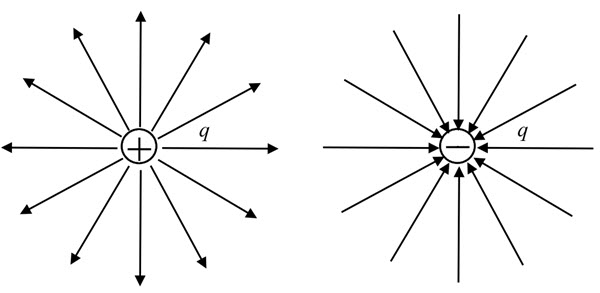
In the above example, a unit test charge ‘q’ placed near a point charge ‘Q’ experiences the force. The direction of this force can be represented by lines that are radially coming out of a positive charge or going in towards a negative charge. These lines of force are called Field Lines or Flux Lines.
Properties of Electric Flux Lines
Electric Field or Flux Lines are the lines of force around a charge with the following properties:
- Flux lines generally originate at positive charges and terminate at negative charges.
- The strength of the electric field is dependent on the number of flux lines.
- All the flux lines are parallel to each other.
- Normally, the flux lines enter or leave a charged surface.
Electric Flux
The Electric Field, imagined to be present around a charge, can be represented in terms of a quantity known as Electric Flux. The field lines or flux lines can be used to pictorially represent the distribution of Electric Flux around a charge.
Based on the experiments performed by Michael Faraday in late 1830’s, Electric Field around a charge can be imagined as presence of lines of force around it. According to his studies, electric field is composed of small bunches of electric lines of force, which are fixed in number.
This bunch or small closed area is called a Tube of Flux. Electric Flux is the total number of tubes of flux in an electric field i.e. Electric Flux is defined as the total number of lines of electric force in any particular electric field. The symbol of Electric Flux is Φ.
Equation of Electric Flux
The concept of flux is always associated with something (electric field, in this case) going through a given area. Then exploring further, the lines of force passing through a surface of a given area is dependent on three factors:
- Strength of the Electric Field
- Area of the Surface
- Orientation of the surface with respect to the lines of force
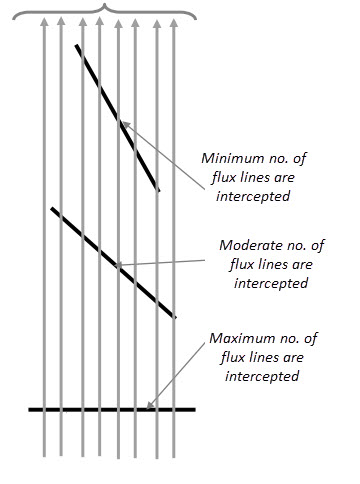
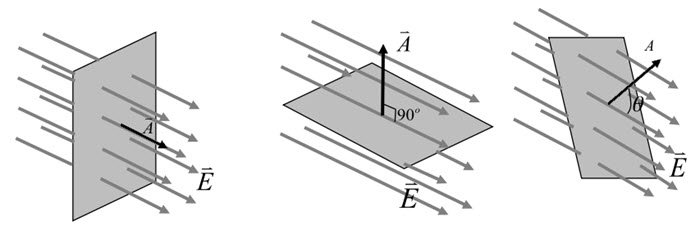
The first two points are pretty obvious but the interesting point here is the orientation of the surface. To understand this more, let us consider a surface, which is inserted through electric field in three different orientations.
When the surface is perpendicular to the electric field, maximum number of lines are intercepted by the surface. If the surface is parallel to the field, then the number of field lines passing through the surface is zero.
But if the surface is placed at an orientation angle of θ, then the number of line passing will be proportional to this angle.
In general, if θ is the angle between the electric field vector and surface vector of the surface with area A, then number of field lines passing through this surface is proportional to cos (θ).
ΦE α cos (θ)
Considering the other two factors i.e. the electric field and the area of the surface, the equation of flux can be written as follows:
ΦE = EAcos (θ)
Where, E is Electric Field with units Newton. Coulomb
A is surface area with units meter2
θ is angle with units degrees or radians
Therefore, the units of Electric Flux are Newton meter2 / Coulomb (Nm2/C).
This formula is well and good if the surface has a deterministic area. What if the surface is curved?
Then the surface is divided into small elements of area d and the integral of the flux is taken for the entire surface.
ΦE = ∫E . dA
Gauss’s Law
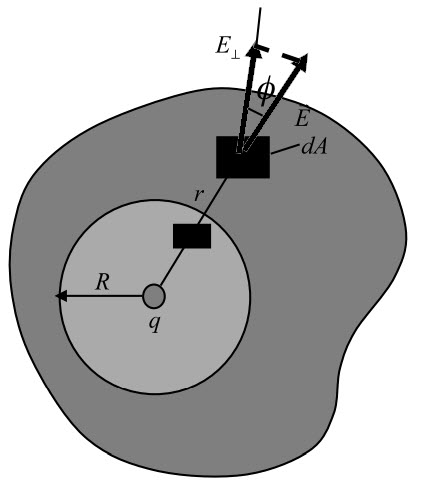
After understanding the concept of Electric Flux, we can say that in a closed surface, if there are no charges inside its volume, then electric flux through the surface is zero. But what if there are some charges inside the volume of the surface? The answer to this lies in Gauss’s Law.
Statement of Gauss’s Law
Gauss’s Law states that the electric flux passing through a closed surface is equal to the ratio of total charge enclosed by that surface to the permittivity of free space.
ΦCLOSED SURFACE = q / ε0
This means that the electric flux passing through a closed surface is independent to shape or area of the surface.
Gaussian Surface
A Gaussian Surface is a special surface over which the Gauss’s Law can be applied. Any Gaussian surface has to satisfy the following conditions.
- The shape of the surface may be irregular but it must be large to enclose the charge.
- It must be a closed surface.
- The magnitude of the field must be constant.
Applications of Gauss’s Law
- Gauss’s Law can be used to find the electric field of point charge, infinite line of charge, infinite sheet of charge or sphere of charge. All these charge distributions are symmetrical in nature.
- We can also use Gauss’s Law to find the electric flux passing through a closed surface.
- The following is the value of electric field calculated using Gauss’s Law for three different distributions of charges:
- Electric Field due to infinite line of charge = λ / 2πε0 r
- Electric Field due to infinite sheet of charge = σ / 2ε0
- Electric Field due to spherical shell = kq / r2