Capacitors are the standard components in electronic circuits. Different combinations of capacitors are used in circuits practically.This article explains about series and parallel combinations of capacitors.
Capacitors in series
How to connect capacitors in Series?
Capacitors in series means two or more capacitors connected in a single line. Positive plate of the one capacitor is connected to the negative plate of the next capacitor.
Here,
QT =Q1 = Q2 = Q3 = ———- = Q
IC = I1 = I2 = I3 = ——— = IN
When the capacitors are connected in series Charge and current is same on all the capacitors.
Why is the charge of capacitors in series the same?
For series capacitors same quantity of electrons will flow through each capacitor because the charge on each plate is coming from the adjacent plate. So, coulomb charge is same.As current is nothing but flow of electrons , current is also same.
What is the equivalent capacitance?
Equivalent capacitance is the overall capacitance of the capacitors. Let us see how to calculate the capacitance when they are in series.
Below is the figure showing three capacitors connected in series to the battery. When the capacitors are connected in series the adjacent plates get charged due to electrostatic induction.
Each plate will have different potential. But the magnitude of charge on the plates is same.
First plate of the C1 will have potential V1 which is equal to the voltage of the battery and second plate will have potential less than V1. Let it be V2.
Now the first plate of C2 will have potential equal to V2 and second plate will have potential less than V3 let it be V4.
First plate of C3 will have potential V5 (V5=V4) and the potential of second plate is less than V5. Let it be V6.
But the overall potential difference between the plates is equal to the emf of the battery.
So VT = V1+V2+V3
But we know that, Q=CV
C=Q/V
Ceq = Q/V1 + Q/V2 + Q/V3 (As charge is same)
1/Ceq = (V1+ V2+ V3 )/Q
VT = Q/Ceq = Q/C1 + Q/C2 + Q/C3
Hence,1/Ceq = 1/C1 + 1/C2 + 1/C3
If N capacitors are connected in series then equivalent capacitance can be given as below.
1/Ceq = 1/C1 + 1/C2 +……… + 1/CN
Thus when the capacitors are in series connection, the reciprocal of the equivalent capacitance is equal to the sum of the reciprocals of the individual capacitance of the capacitors in the circuit.
Capacitors in Series Example
Calculate the equivalent capacitance and the individual voltage drops across the set of two capacitors in series have 0.1uF and 0.2uF respectively when connected to a 12V a.c. supply.
Equivalent capacitance,
1/Ceq = 1/C1 + 1/C2
Ceq = (C1C2) / (C1 + C2)
Ceq = (0.1uF*0.2uF) / (0.1uF+0.2uF)
Ceq = 0.066uF = 66nF
Voltage drops across the two given capacitors in series are,
V1 = (C2*VT)/ (C1+C2) = (0.2uF*12V)/ (0.1uF+0.2uF) = 8Volts
V2 = (C1*VT)/ (C1+C2) = (0.1uF*12V)/ (0.1uF+0.2uF) = 4Volts
From these results we observed that the equivalent capacitance 66nF is less than the smallest capacitance 0.1uF of the given two capacitors. The individual voltage drops across the given two capacitors are different.
But the sum of individual voltage drops of both the capacitors is equal to the total voltage. i.e 8V+4V=12V.
Now we calculate the charge stored in individual capacitor,
Q1 = V1* C1 = 8V * 0.1uF = 0.8uC
Q2 = V2* C2 = 4V * 0.2uF = 0.8uC
Here we observed that equal charge 0.8uC is stored in both the capacitors C1 and C2 which are connected in series.
Capacitors in Series Summary
• Charge on the capacitors is same in series connection.
• Equivalent capacitance of the capacitors is less than the smallest capacitance in series.
• Equivalent capacitance of n capacitors in series is given as
1/Ceq = 1/C1 + 1/C2 +……… + 1/CN
Capacitors in Parallel Circuits
Why do we connect capacitors in parallel?
There is an advantage of connecting capacitors in parallel than in series. When the capacitors are connected in parallel the total capacitance value is increased. There are some applications where higher capacitance values are required.
How to connect capacitors in Parallel?
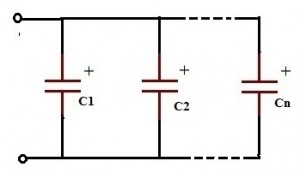
Below figure shows the connection of capacitors in parallel. All the positive terminals are connected to one point and negative terminals are connected to another point.

What is Equivalent capacitance of the capacitors in parallel?
- All the capacitors which are connected in parallel have the same voltage and is equal to the VT applied between the input and output terminals of the circuit.
- Then, parallel capacitors have a ‘common voltage’ supply across them .i.e. VT = V1 = V2 etc.
- The equivalent capacitance, Ceq of the circuit where the capacitors are connected in parallel is equal to the sum of all the individual capacitance of the capacitors added together.
- This is because the top plate of each capacitor in the circuit is connected to the top plate of adjacent capacitors.In the same way the bottom plate of each capacitor in the circuit is connected to the bottom plate of adjacent capacitors.
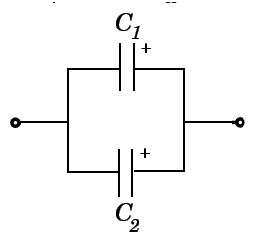
Let us see how to calculate the equivalent capacitance of capacitors when connected in parallel.Consider two capacitors connected as shown in the below circuit.
The total charge (Q) across the circuit is divided between the two capacitors, means the charge Q distributes itself between the capacitors connected in parallel. charge Q is equal to the sum of all the individual capacitor charges.
Thus Q=Q1+Q2
Where Q1,Q2 are charges at capacitors C1 And C2.
We know that,
Q=Ceq VT
Here, Q = Q1+Q2
Ceq VT = C1xV1+C2xV2
Since VT = V1 = V2 = V
Ceq VT = C1xV+C2xV
Ceq VT = (C1+C2)V
Hence Ceq=C1+c2
If N capacitors are connected in parallel then Ceq=C1+C2+C3+——Cn
Thus equivalent capacitance of the capacitors which are connected in parallel is equal to the sum of the individual capacitance of the capacitors in the circuit.
Capacitors in Parallel Example No1
Consider the capacitance values of the two capacitors C1 =0.2uF and C2 =0.3uF which are shown in above figure 4. Now calculate the equivalent capacitance of the circuit.
We know that the Equivalent capacitance,
Ceq = C1 + C2
Ceq =0.2uF + 0.3uF
Ceq =0.5uF
One important point to remember about parallel connected capacitor circuits, the equivalent capacitance (Ceq) of any two or more capacitors connected together in parallel will always be greater than the value of the largest capacitor in the circuit as we are adding together values. So in our example above Ceq =0.5uF whereas the largest value capacitor in the circuit is only 0.3uF.
When capacitors are connected in parallel?
Here are some applications where capacitors are connected in parallel.
- In some DC supplies for better filtering small capacitors with superior ripple factor are used. These are connected in parallel to increase the capacitance value.
- This can be used in automotive industries in large vehicles like trams for regenerative braking. These application may require large capacitance values than the capacitance usually available in the market.
Capacitors in parallel Summary
- Voltage on the capacitors is same when connected in parallel. The equivalent voltage of the parallel capacitors is equal to the smallest voltage rating capacitor in parallel.
- The overall capacitance value of the capacitors is sum of all the capacitance values connected in parallel.
- Equivalent capacitance of n capacitors in parallel is Ceq=C1+C2+C3…Cn.


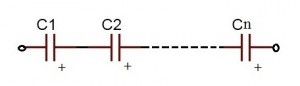


2 Responses
It’s very important to improve my knowledge
This work is good and simple to understand.