Inductors are said to be connected in parallel when two terminals of an inductor respectively connected to each terminal of other inductors or inductor. Similar to the parallel connection of resistors, the total inductance in parallel connection of inductors is somewhat lesser than smallest inductance of an inductor in that connection.
When the inductors are connected in parallel, the current flow through each inductor is not exactly equal to the total current, but the sum of each individual current through parallel inductors gives the total current (as it divides among parallel inductors).
If the current flow through the each inductor is less than the total current, the magnetic field generated by each inductor is also less than that of field generated by total current through it.
In case of resistors in parallel, most of the current flows through the smallest resistor as it offer the least opposition to the current flow than larger resistor.
Likewise, if the inductors are connected in parallel, current chooses least opposition path of inductor when current in that circuit is decreased or increased while each inductor individually opposes that change (increase or decrease of current).
Outline
ToggleInductors in Parallel
Inductors, in the parallel connection, the voltage across each inductor is equal and also if the total current is changed, the voltage drop across each individual inductor will be less as compared with series connection. For a given rate of change of current, less will be the inductance in less voltage.
These are the basic points to be considered in parallel connection of inductors. Now we will discuss the parallel connection of inductors with and without considering mutual coupling between these inductors.
Inductors Connected in Parallel (Without Magnetic Coupling)
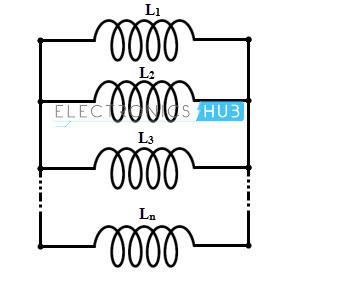
As we discussed above, one end of inductors is connected to a node and other ends of inductors are collectively connected to another node in parallel connection. The parallel connection of n inductors is shown in below figure.
Consider that there is no magnetic coupling between inductors and hence the total inductance equal to the sum of reciprocals of the individual inductances. Let us discuss how this statement can be obtained.
We know that, in a parallel network the voltage remains constant and the current divides at each parallel inductor. If IL1, IL2, IL3 and so on ILn are the individual currents flowing in the parallel connected inductors L1, L2 and so on Ln, respectively, then the total current in the parallel inductors is given by
ITotal = IL1 + IL2 + IL3 . . . . + In
If the individual voltage drops in the parallel connection are VL1, VL2, VL3 and so on VLn, then the total voltage drop between the two terminals VT is
VTotal = VL1 = VL2 = VL3 . . . . = Vn
The voltage drop in terms of self inductance can be expressed as V = L di/ dt. This implies total voltage drop,
VT = LT di/dt
⇒ LT d/dt (IL1 + IL2 + IL3 . . . . + In)
⇒ LT ( (di1)/dt + (di2)/dt + (di3)/dt . . . .)
Substituting V / L in place of di/dt, the above equation becomes
VT = LT (V/L1+ V/L2 + V/L3 . . . .)
As the voltage drop is constant across the circuit, then v = VT. So we can write
1/LT = 1/L1 + 1/L2 + 1/L3 . . . . .
This means that the reciprocal of total inductance of the parallel connection is the sum of reciprocals of individual inductances of all inductors. The above equation is true when there is no mutual inductance is affect between the parallel connected coils.
For avoiding complexity in dealing with fractions, we can use product over sum method to calculate the total inductance. If two inductors are connected in parallel, and if there is no mutual inductance between them, then the total inductance is given as
LT = (L1× L2)/(L1+ L2)
Example of Inductors Connected in Parallel
If a circuit has 2 inductors of 20 Henry and 30 Henry connected in parallel, what will be the total inductance of the parallel arrangement?
Sol: We know that the formula for total inductance of series, 1/LT = 1/L1+ 1/L2
Given that L1 = 20 Henry
L2 = 30 Henry
LT = (L1* L2)/(L11+ L2 ) = ((20*30))/((20+30) ) = 600 / 50 = 12
The total inductance is LTotal = 12 Henry.
Mutually Coupled Inductors in Parallel
When there exist magnetic coupling between the inductors, the above derived formula for total inductance must be modified because total inductance can be more or less depending on the magnetic field directions from each inductor. The magnetic flux produced by the parallel connected inductors will link with each other.
When the fluxes produced are in the same direction of magnetic flux, the mutual inductance will increase; these coils are called “Aiding” coils. If the flux is in opposite direction to the magnetic flux, the mutual inductance will decrease; these coils are called “Opposing” coils. This mutual inductance will depend upon the placed distance of two coils.
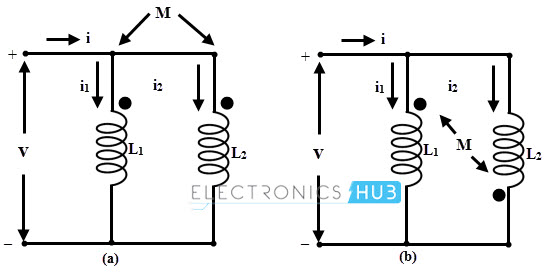
Consider that two inductors are connected in parallel with self inductances L1 and L2, and which are mutually coupled with mutual inductance M as shown in below figure.
Parallel Aiding Inductors
Consider the figure (a), in which inductors L1 and L2 are connected in parallel with their magnetic fields aiding. The total current through the circuit is given as
i = i1 + i2
di/dt = (di1)/dt + (di2)/dt …………. (1)
The voltage across the inductor or parallel branch is given as
V = L1 (di1)/dt + M (di2)/dt or L2 (di2)/dt + M (di1)/dt
L1 (di1)/dt + M (di2)/dt = L2 (di2)/dt + M (di1)/dt
(di1)/dt (L1– M) = (di2)/dt (L2– M)
(di1)/dt = (di2)/dt ((L2 – M))/((L1 – M)) …………. (2)
Substituting equation 2 in equation 1, we get
di/dt = (di2)/dt ((L2– M))/((L1– M)) + (di2)/dt
di/dt = (di2)/dt { (L2– M))/((L1– M)) + 1} …………. (3)
If LT is the total inductance of the parallel inductor circuit , then voltage is given by
V = LT di/dt
LT di/dt = L1 (di1)/dt + M (di2)/dt
di/dt = 1/ LT { L1 (di1)/dt + M (di2)/dt }
Substituting equation 2 in above equation, we get
di/dt = 1/ LT { L1 (di2)/dt (L2– M))/((L1– M)) + M (di2)/dt }
di/dt = 1/ LT { L1 (L2– M))/((L1– M)) + M }(di2)/dt …………. (4)
Equating equations 3 and 4 we get
(L2– M))/((L1– M)) + 1 = 1/ LT { L1 (L2– M))/((L1– M)) + M }
Simplifying the above equation, results
LT = (L1 L2– M2)/(L1+ L1 )-2M)
Here 2M represents the magnetic flux of L1 on L2 or L2 on L1. If the magnitude of two inductances is equal with a perfect magnetic coupling between them, the equivalent inductance of two inductors is L because LT = L1 = L2 = M. In such case, if the mutual inductance is zero, the total inductance would be L ÷ 2.
Parallel Aiding Inductors Example
If the two inductors 25mH and 45mH are connected in parallel aiding, calculate the total inductance of the parallel combination. The mutual inductance is given as 20mH.
SolGiven that, L1 = 25 mH
L2 = 45 mH
M = 20 mH
Applying the formula for total inductance of aiding inductors, LT = (L1 L2– M2)/(L1+ L1 )-2M)
LT = (25*45- 202)/(25+45-2*20)
= (1125-400)/(70-40)
= 725/30
= 24.166mH
Therefore the total inductance is 24.166 milli Henry.
Parallel Opposing Inductors
Similarly, if we consider the figure (b), in which inductors L1 & L2 are connected in parallel with their magnetic fields opposing, the total inductance is given as
LT = (L1 L2– M2)/(L1+ L2)+ 2M)
In opposing parallel inductors, if the magnitudes of two inductances are equal with the perfect magnetic coupling, the equivalent inductance of two inductors will be zero, as they cancel each other. If two inductors effectively allows the current to flow through them, the total inductance is given as (L ± M) ÷ 2.
Parallel opposing Inductors Example
Ex: If the two inductors 25mH and 45mH are connected in parallel opposing, calculate the total inductance of the parallel combination. The mutual inductance is given as 20mH.
Sol: Given that, L1 = 25 mH
L2 = 45 mH
M = 20 mH
Applying the formula for total inductance of aiding inductors, LT = (L1 L2 M2)/(L1+ L2 )+2M)
LT = (25*45-202)/(25+45+2*20)
= (1125-400)/(70+40)
= 725/110
= 6.59mH
Therefore the total inductance is 6.59 milli Henry.
Summary
- Connecting the two terminals of inductor respectively to other inductor or inductors terminals, then that connection is referred as “parallel connection of inductors”.
- When the fluxes produced by individual inductors are in the same direction, the mutual inductance will be increased; then these coils are called “Aiding” coils. Total inductance for aiding coils is LT = (L1 L2– M2)/(L1+ L2 )-2M).When the fluxes produced by individual inductors are in the opposite direction of magnetic flux, the mutual inductance will be decreased; then these coils are called “opposing” coils. Total inductance for aiding coils is LT = (L1 L2– M2)/(L1+ L2 )+2M)




4 Responses
Please check braces in formulas. Sometimes are doubled, for example: ((20*30))
And sometimes are not in pair, for example: LT = (L1 L2 M2)/(L1+ L2 )+2M)
Thank you for the refresher course. It’s been a long time since I studied that.
That…….was the best yet simplest derivation……Thanku…..whoever put it …..
How to Calculate the inductance if more than 2 inductors are given in parallel with mutual inductance of each with everyone