The term ‘Harmonics’ is related to the fundamental frequency of a waveform. Before learning about harmonics, we should be familier with some of the concepts of wave forms. Let’s discuss about the topics Natural frequency and forced frequency.
Outline
ToggleDifferent Harmonic Frequencies
Natural frequency
When a body is vibrating freely without any external forces applied on it, then the vibrations are called “Natural vibrations”. The frequency at which the natural vibrations occur is called “Natural frequency”.
Forced frequency
When a body is oscillating by applying an external periodic force, the vibrations are called “ Forced vibrations”. The frequency of the forced vibrations is called “Forced frequency”.
Progressive waves
When a wave continuously moves forward in a medium without being reflected at any point in the path, it is called “Progressive wave”.
Standing waves
When two progressive waves of the same frequency and amplitude travel through a medium in opposite directions, then they are super imposed. The super imposed wave is called “Standing wave”. In standing waves we find nodes and antinodes.
Fundamental Frequency
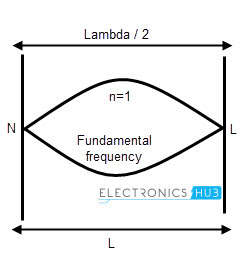
It is defined as the lowest frequency of a periodic waveform. It is generally denoted as ‘f’. In other words, the lowest resonating frequency of a vibrating object is called as “Fundamental frequency”.
What is Harmonic?
Harmonic is a frequency, which is an integer multiple of the fundamental frequency. The forced resonance vibrations of an object are caused to produce standing waves. At the natural frequency , it forms a standing wave pattern. These patterns are created at specific frequencies, they are called “Harmonic Frequencies” or “Harmonics”.
The sound produced by a wave form at its harmonic frequency is very clear, and at other frequencies we get noise, and cannot hear the clear sound of waves.
Harmonics may occur in any shaped wave forms, but mostly they occur in sine waves only. Non – sinusoidal wave forms, like triangular and saw tooth wave forms are constructed by adding together the harmonic frequencies. The word “harmonic” is generally used to describe the distortions caused by different un- desirable frequencies called “noise”, of a sine wave.
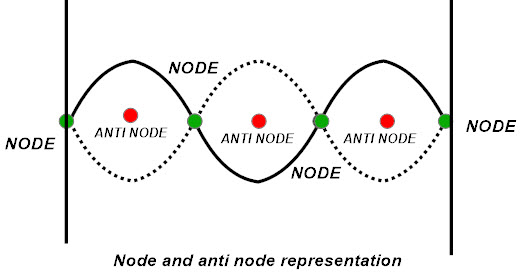
In every harmonic, we find two positions, they are nodes and anti nodes.
Node
Nodes are the points that appear to be still standing along the medium. They do not have displacement. So they are referred as points also called nodes.
Antinodes
There are the particles that undergo maximum displacement between two points. The two points are nodes. Here one node is positive and other is negative. The nodes and antinodes are shown in the below figure.
Node and antinodes occur in a wave form. So the waves have harmonic frequency in them. The fundamental frequency is the smallest frequency in a harmonic. Hence there is only a single anti-node occurs between them. This Antinode is middle of the two nodes. So from this we can say that the guitar string produces longest wavelength and the lowest frequency.
The lowest frequency produced by any instrument is called the fundamental frequency. This is also known as “first harmonic” of the wave. In words of fundamental frequency we can say that harmonics are the integer multiples of the fundamental frequency.
Ex: f,2f,3f,4f etc… are Harmonics.
Because of multiple integers of fundamental frequency, we will have n number of harmonics like 1st harmonic, 2nd harmonic,3rd harmonic etc…
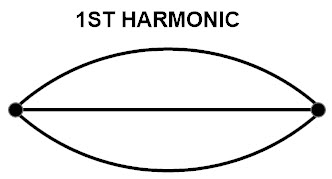
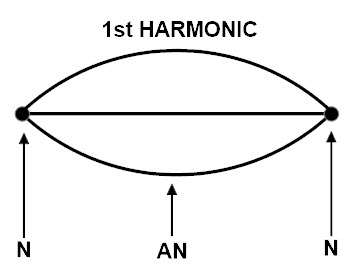
First harmonic
As we discussed earlier, the fundamental frequency is also called as First harmonic. In the first harmonic we have two nodes and one anti -node.
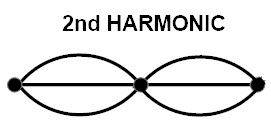
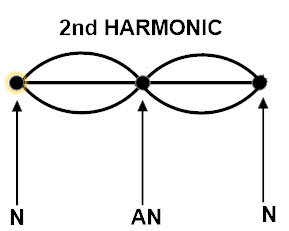
Second harmonic
The second harmonic consists of 3 nodes and two antinodes. If we set a node between two nodes of the first harmonic, we can have the second harmonic. In the first harmonic, the second node will be between two nodes, first and last.
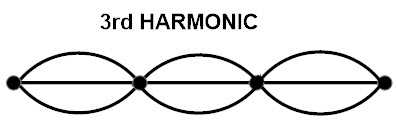
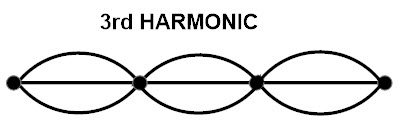
Third harmonic
For the third harmonic if a node is kept at the both ends of a sting the resulting wave pattern consists of four nodes and 3 antinodes. This means the wave form at third harmonic has a full sinusoidal wave cycle and one half cycle. The diagram is as shown below.
By observing the above discussion, we can say that the numbers of antinodes are equal to the integer multiples of specific harmonics. i.e., for 1st harmonic we have 1 antinode, for 2nd harmonic we have 2 antinodes etc.
Harmonic frequencies can be calculated by using the formula
Speed=frequency x wavelength
V = n x λ
nth harmonic = n x fundamental frequency
If we know the speed and wavelength of a wave form, we can calculate harmonic frequency. There are two types of harmonics in waves, they are even harmonic and odd harmonics. For example, a cylinder with both sides open will vibrate at both even and odd harmonics, but a cylinder with one closed side will vibrate at only odd harmonics.
Characteristics of Harmonics
Most of the oscillations we hear are caused by Harmonics. For example, the music sounds like guitar, violin and even the human voice. The harmonics are also called as Harmonic partials. The characteristics of harmonics will depend on oscillations of the instrument or wave form.
So generally oscillations are the reason for producing Harmonics. An oscillator is nothing but moving or vibrating instrument. Partial harmonics will produce a different frequency than that of full Harmonics. But the exact harmonic frequency will produced by a long length and thin wired instruments.
They produce only one harmonic exactly. The frequencies which will occur at the multiple integers of fundamental frequency are called harmonic frequencies.
The human ear does not clearly audible of all harmonics.The frequencies other than harmonic frequencies are called inharmonic frequencies. In this, many harmonics are combined to form as a sound. The inharmonic sounds are audible to the human ear.
Ex: The first is, Our school bell and church bell, we see regularly. Second, Antique singing bowls are other examples that vibrate only at harmonic frequencies . Another important characteristic property of harmonics is it that, all harmonics are periodic at fundamental frequency, and then the sum of harmonics is also periodic at fundamental frequency.
Harmonics and Overtones
The frequency which is higher than the fundamental frequency is called as “Overtone”. Generally overtones exist in musical instruments. The over tones will depend on the tone of the musical instrument. As the tone will differ from one musical instrument to other, the occurance of over tones will also differ. On mixing / combining the overtones, we can acquire the fundamental tone of an instrument.
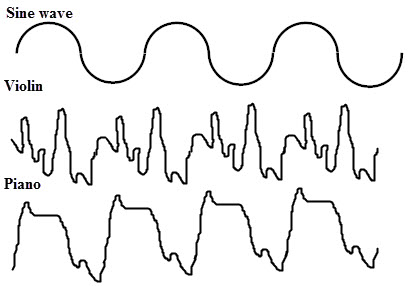
Observe the above sound outputs produced by different instruments, violin and piano. They have the same frequency, so they have the same note, their overtones are different, and ultimately their sounds are also different. This means the overtones of an instrument can affect its sound output. Violin’s jagged waveform denotes a sharper sound, while the piano produces a purer sound which is closer to a sine wave.
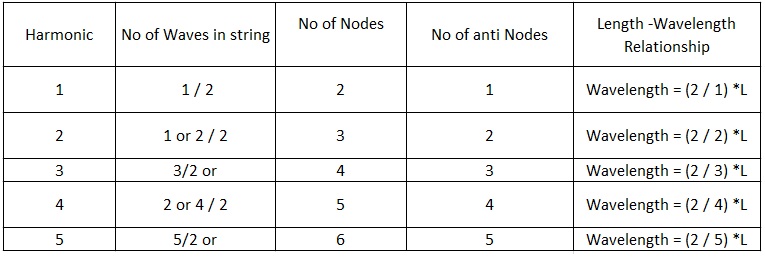
Length Wave Length Relationship
In order to get the length and wavelength relationship we will again see all harmonics. I.e., first, second, third harmonics. We all know that the wavelength of a sine wave is ‘lambda’. The harmonics are also represented as sine waves. Let us calculate
From first harmonic
So in first harmonic the two ends of a string are fixed they are called as nodes. And when there are vibrations the wire moves up and down, creating an antinode. So this figure is like a semi sinusoidal. So one-half of the wavelength
From second harmonic
In second harmonic there are two antinodes so there are two loops. From first harmonic we already calculated one loop is equal to one half wavelength.so here there are two loops totally one wavelength.
From third harmonic
In third harmonic motion there are three loops and each loop consists of one half wavelength.so all the three loops sum is 3/2 of lambda
From all these harmonics we can say that for 1st harmonic we have one antinode, for second harmonic 2 antinodes are there, for third harmonic 3 antinodes. So for nth harmonic there are n antinodes.
So by deriving the formula for length and wavelength relation we get
L=n/2 of a wavelength
Also, we can write these formulas as shown below
For 1st harmonic: L=1/2-lambda
For 2nd harmonic: 2L=2/2-lambda
For 3rd harmonic: 3L=3/2-lambda
Like this for nth harmonic: nL=n/2-lambda Where ‘n’ is an integer.
The length and wavelength relationship in harmonics and also the mathematical relationship also given below in tabular format
L=n/2 (lambda)
Disadvantages of Harmonics
- Harmonics will affect the performance of the power systems. The disadvantages of harmonics are listed below.
- Harmonics will degrade the quality of the electrical power supply in the distribution network. It may cause several negative effects.
- The harmaonics may cause to increase the effective RMS current, this results in power loss of the distribution system.
- The cumulative increase in the third harmonic will cause the overloading in the neutral conductors.
- The harmonics will cause to increase in the noise level of an electrical signal.
- Harmonics can disturb the supply voltage, so that they are caused to the wrong operation of the sensitive loads.
- Harmonicas causes the disturbances in the communication lines and the telephone lines.
- They affect the resonance between the supply inductance and the capacitance level of the power factor capacitors.
In brief, the harmonics will cause the following errors in power system and tele – communication systems.
- Equipment heating
- Equipment malfunction
- Equipment failure
- Communications interference
- Fuse and breaker mis-operation
- Process problems
- Conductor heating.
Harmonics Examples
We already know that we come across many harmonic frequencies in our daily life, here we see some examples for harmonics
Example
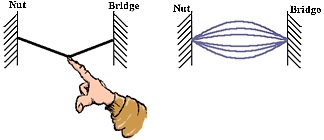
Many oscillators like a plucked guitar string will oscillate at many frequencies, but they are not harmonics, they are usually called partial harmonics. So when we take a long and thin oscillator, the frequencies will occur in harmonic range. To know the exact position of occurance of the harmonics, primarily we should calculate the fundamental frequency of the wave form.
Let us take a guitar string that produces harmonic frequencies. Then keep the string ends attached and fix it in a guitar structure. So the ends are unable to move. So already we know that harmonic waves are produced by standing waves. For them there is a node and antinode.
Here we have the two ends are nodes and hence there are nodes there is also antinode. so there is a harmonic frequency in itself. So the fundamental frequency is the smallest frequency, Hence there is one antinode between them. This Antinode is middle of the two nodes. So from this we can say that the guitar string produces longest wavelength and the lowest frequency.
The lowest frequency produced by any instrument is called the fundamental frequency. This is also called first harmonic.