Mathematically, a complex number is the combination of real number and imaginary number. The Phasor is represented by a complex number in complex number plane.
This complex number representation gives magnitude and phase of a sine wave, with which we can analyze the characteristics of a circuit. Sinusoidal waveforms are functions of time and are represented in time domain.
Usually, phasor transform method is used for solving the equations related to the waveforms that transform the functions of time t to functions of radian frequency w.
Frequency domain equations are algebraic equations which are easier to solve compared to time domain equations which are partial differential equations.
Thus, the complex number representation facilitates easy solving of algebraic equations for the unknown phasors. Let us discuss complex numbers and their manipulating techniques.
Outline
ToggleCOMPLEX NUMBERS
Imaginary numbers are square roots of negative real numbers. Imaginary number consists of imaginary unit or j operator which is the symbol for √-1. This j operator used for simplifying the imaginary numbers. Consider √- 4 which can be simplified as √-1 × √ 4 = j√4 = j2.
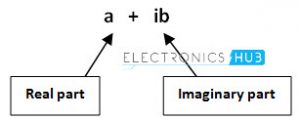
The manipulation of complex numbers is more complicated than real numbers, that’s why these are named as complex numbers. A complex number consists of two parts, namely a real part and imaginary part which are connected by a plus or a minus sign as shown below.
Example:
The imaginary part of a complex number is called “Imaginary number”. We denote that by the English alphabet ‘i’ (the lower case) or j. We pronounce that as ‘i- operator’. An i operator is placed before the imaginary number to signify the imaginary part. Ex: i3, i432, i6 etc.
The complex numbers are represented in 2 dimensional Cartesian plane. This is also called “S plane”. The axes are called “Horizontal axis” and “Vertical axis”. The vertical axis is also called “Real axis” and it is denoted by Y. It represents the range of magnitude or voltage of sine wave.
Similarly, the horizontal axis is called “Imaginary axis”. It is denoted by X. It represents the time period and the phase difference of sine wave. In graphical method we represent the real and imaginary axes of complex number as Re(Z) and Im(Z), where Z is the complex number in the rectangular form, Z = a + ib.
Here the real part of a complex number is also called as “Active part” and imaginary part is called as “Reactive part”.
Rules for mathematical operations of complex numbers
- For addition and subtraction: In addition and subtraction operations of imaginary numbers, we use general mathematical rules as real numbers i.e. on adding or subtracting of two imaginary numbers, we get another imaginary number. Ex: i9 + i5 = i14.
- For multiplication: multiplication of imaginary number follows a different rule. That is, if any two imaginary are multiplied, we get a real number. Ex: i2 * i3 = 6.
NOTE: We can also write the real number as complex number by making the coefficient of imaginary part as ‘0’.
Ex: 6 can be written in complex number as 6 + i0.
Vector Rotation of i- Operator
Generally, electrical voltages and currents and their phase relations are represented by electrical vectors, where length of the vector represents the magnitude of that quantity involved while direction with respect to reference axis represents a lapse in time between positive maximum values of voltage and current.
In order to specify these vectors in terms of its x and y components, i operator is used to distinguish between x-axis and y-axis projections.
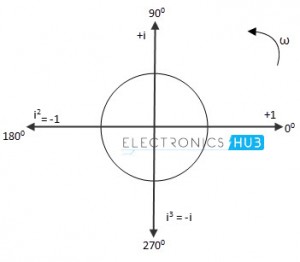
This is because y-axis projection is +900 from the x-axis projection. This i operator rotates the vector without altering its magnitude. Therefore, when +i operator is applied as multiplying factor for a vector, it produces 900 counter clockwise rotation and -i operator produces 900 clockwise rotation of any vector to which it is applied as multiplying factor.
Successive multiplication of +i operator to a vector will produce successive 900 steps of rotation of the vector in counter clockwise direction without affecting the magnitude of that vector.
Similarly, successive multiplication of -i operator to a vector will produce successive 900 steps of rotation of the vector in clockwise direction as given in below.
i1 = √-1 = +i » rotates vector 900 (Counter clockwise)
i2 = i * i = (√-1)2 = -1 » rotates vector 1800 (Counter clockwise)
i3 = i2 * i = (√-1)3 = -i » rotates vector 2700 (Counter clockwise)
i4 = i3 * i = (√-1)4 = +1 » rotates vector 3600 (Counter clockwise)
Similarly for clockwise rotation is represented as
-i1 = -√-1 = -i » rotates vector -900 (clockwise)
-i2 = -1 » rotates vector -1800 (clockwise)
– (i) 3 = √-1 » rotates vector -2700 (clockwise)
– (i) 4 = 1 » rotates vector -3600 (clockwise)
Complex Numbers Representation
Mostly, complex numbers are represented by two methods, they are
- Cartesian or Rectangular form
- Using S- plane
Complex Numbers Using Rectangular Form
As discussed earlier, a complex number is represented as Z = a + ib in rectangular form.
Where , Z is complex number
a is a real part of the vector
b is a imaginary part of vector
and i is the coefficient of imaginary part. Its value is √-1.
Ex: If Z = 2 + i3 then ‘2’ represents real part and ‘3’ represents imaginary part.
Complex Numbers Using Complex or S-Plane
In S- plane representation method, a complex number is represented as a point in Cartesian plane or S- plane. For example, consider Z = 2 + 4i, in which 2 is real part and 4 is imaginary part. It is represented in S- plane as shown below.
Here the real part of complex number (2) is represented by a line drawn 2 units out from the origin on positive horizontal axis. The imaginary part (4i) is represented by a line extended 4 units from the origin on positive vertical axis.
Thus imaginary values are always assumed to be drawn along Y-axis or vertical axis and the real values drawn along x-axis or horizontal axis.
Four Quadrant Argand Diagram
If a real number is multiplied by -1, it results to move the point from one side of origin to other. Suppose if +2 are multiplied by -1 or j2, the new position is equivalent to a rotation through 1800 from old position.
This concept of multiplying by j as vector rotation is the basis for using complex numbers in alternating current circuits. This concept leads to a diagram called the Argand diagram which represents the complex numbers.
In Argand diagram, the real part of complex number is represented on X axis i.e. Re (z). The imaginary part of the complex number is represented on Y axis i.e. Im (z). In Cartesian plane, the complex number is defined as (a, b).
On the Argand diagram, the horizontal axis represents all positive real numbers to the right of the vertical imaginary axis and all negative real numbers to the left of the vertical imaginary axis. Positive imaginary numbers are represented above the origin and negative imaginary numbers are represented below the origin, on the vertical axis.
In the same way, all the positive real numbers are represented in the right side of the origin and all negative real numbers are represented in the left side of the origin, on the horizontal axis. So a complex plane with 4 coordinates is formed.
The Argand diagram is used to represent the phasor rotation where the length of the vector is equal to the magnitude of the complex number. It completes a full cycle for every 2π/ω seconds.
00 = ± 3600 = + 1 = 1 ∠00 = 1 + i0
+ 900 = + √-1 = + i = 1 ∠+900 = 0 + i1
– 900 = – √-1 = – i = 1 ∠-900 = 0 – i1
± 1800 = (√-1)2 = – 1 = 1 ∠± 1800 = – 1 + i0
Complex numbers with zero real part is called “Pure imaginary number”. Ex: Z = 0 + i2.
Complex numbers with zero imaginary part is called “Pure real number”. Ex: Z = 2 + i0.
Angle and quadrant
00 to 900 → first quadrant (I).
900 to 1800 → second quadrant (II).
1800 to 2700 → third quadrant (III).
2700 to 3600 → fourth quadrant (IV).
We can find the relevant phase angle of the complex number by using
tan-1 (imaginary component ÷ real component)
The Argand sketch for the complex numbers in all the 4 quadrants is given below.
| 1 |  | a is positive b is positive Argument is positive | Ø=tan-1[b/a] |
| 2 | 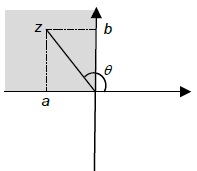 | a is negative b is positive Argument is positive | Ø=π+tan-1[b/a] |
| 3 | 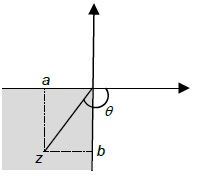 | a is negative b is negative Argument is negative | Ø= -π+tan-1[b/a] |
| 4 | 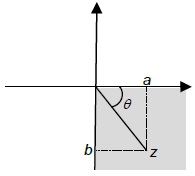 | a is positive b is positive Argument is negative | Ø= tan-1[b/a] |
Addition and Subtraction of Complex Numbers
If it is needed to perform mathematical operations like addition or subtraction on complex numbers, first we have to split the complex number into real part and imaginary part.
For the addition of two complex numbers, add the real parts and add imaginary parts.
If the first complex number is P = a + ib and the second complex number is Q = x + iy , then the sum of two complex numbers is given as
P + Q = (a + x) + i (b + y)
P + Q = (a – x) + i (b – y)
Similarly, to subtract two complex numbers, we subtract the real parts and subtract the imaginary parts.
The difference of two complex numbers is given as
P + Q = (a – x) + i (b – y)
Example
Find the sum and difference of given two complex numbers. A = 2 + i4 and B = 4 +i3.
Addition
P + Q = (2 + i4) + (4 + i3)
= (2 + 4) + i (4 + 3)
= 6 + i7
Subtraction
P + Q = (2 + i4) – (4 + i3)
= (2 – 4) + i (4 – 3)
= -2 + i1
Graphical Addition and Subtraction
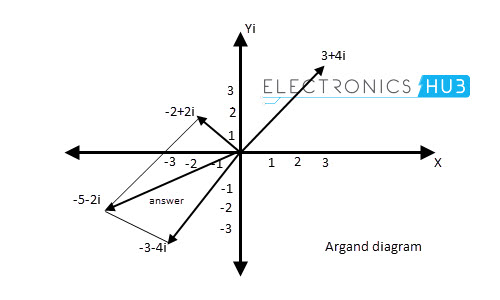
The method of adding complex numbers is same as addition of two vectors using parallelogram of vectors. The below figure illustrates the addition method of 3 + 4i and -4 + 2i complex numbers using graphical method.
Subtraction of (3 + 4i) from (-2 + 2i) in graphical method is illustrated in below figure.
Multiplication and Division of Complex Numbers
Complex numbers are multiplied in the same manner that binomial multiplies and remember that j2 = -1.
Consider two complex numbers (a+bi) and (c+di), then its multiplications is given as
(a+bi) x (c+di) = a (c+di) + bi (c+di)
= ac + adi + bci + bd i2
= ac + adi + bci + bd (-1)
= ac + adi + bci – bd
= (ac – bd) + (ad i + bc i)
= (ac -bd) + (ad + bc) i
Suppose if two complex numbers are (2 + 3i) and (4 + 5i), then its multiplication is
(2 + 3i) x (4 + 5i) = 2(4 + 5i) + 3i (4 + 5i)
= 8 + 10i + 12i + 15i2
= 8 + 22i + 15(-1)
= 8 + 22i -15
= -7 + 22 i
DIVISION
Complex numbers are divided in the same manner that binomials are divided containing radical in the denominator. It involves in finding the conjugate of the denominator.
Let’s see an example for division of complex numbers.
Example
(4 + 2i) ÷ (3 – i)
((4 + 2i))/((3 – i) )= ((4 + 2i))/((3 – i) )× ((3+ i))/((3+ i) )
= (12+4i+6i+2i2)/(9+3i-3i-i2 )
= (12+10i+2 (-1))/(9-(-1))
= (10+10i)/10
= (1+i)/1
= 1 + i
Therefore, (4 + 2i) ÷ (3 – i) = 1 + i.
Complex Conjugate
The complex conjugate of a complex number is the same number except the sign of the imaginary part is changed. The complex number obtained by reversing the sign of the imaginary number.
The sign of the real part become unchanged while finding the conjugate. The conjugate complex number is represented by the symbol z*.
For example, the complex conjugate of Z = 4 + i5 is z* = 4 – i5
The complex number and its conjugate will have same magnitude and they have same horizontal position on the X axis, but their vertical positions exactly opposite in Argand diagram.
Things to remember about conjugate
- The sum of complex number and its conjugate is always a real number (active component).
(4 + i5) + (4 – i5) = 8 (a real number) - The subtraction of complex number and its conjugate is always an imaginary number (reactive component).
(4 + i5) – (4 – i5) = 10i (an imaginary number) - Usually, the complex conjugate number is used to find the apparent power of an alternating circuit in rectangular form.
Complex Numbers using Polar Form
Complex numbers can be represented in polar and rectangular forms. As discussed above, rectangular form of complex number consists of real and imaginary parts. In case of polar form, a complex number is represented with magnitude and angle i.e. Z
A ∠ ±θ. Here A is the magnitude of the vector and θ is the phase angle. It may be positive or negative.
Polar Form Representation of a Complex Number
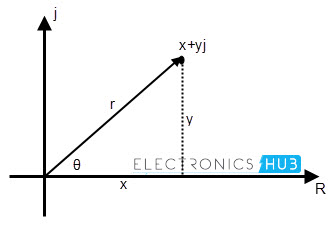
Expressing a complex number in polar form use basic trigonometric concepts of triangle and Pythagoras’s theorem to find the magnitude and the angle made with axis.
The polar form representation of complex number x + iy in the Cartesian plane is shown in above figure. Here r is the resultant vector or diagonal of the triangle, formed by the complex number.
By applying Pythagoras’s theorem, we get
Z2 = x2 + y2
Z = √(x2 + y2)
The vector components can be written as, x = Z cos θ and y = Z sin θ.
The angle made with the real axis is given as
θ= tan-1y⁄x
The polar form represents the length and angle of the complex number. The complex number and its conjugate have same magnitude (modulo) and they have opposite angle.
Ex: The complex number 5 ∠600 and its conjugate number 5 ∠-600 have same magnitude.
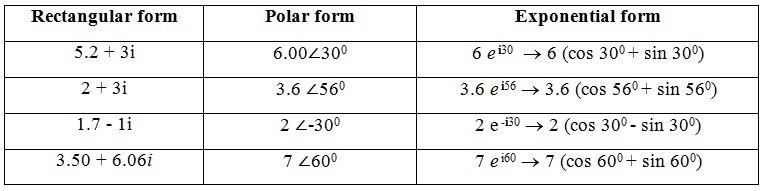
Conversions of Complex Number
While analysing the electronic circuits, it is needed to convert complex numbers from one form to another form. In rectangular form, we represent the real part and imaginary parts of a complex number on real axis (Horizontal axis) and imaginary axis (Vertical axis) respectively.
But in polar form, the complex number is simply represented as A ∠θ. Now let’s us learn about the relationship and conversions of polar form and rectangular form and vice versa.
Conversions of Polar Form to Rectangular Form (P → R)
The conversion of polar to rectangular form involves in finding the trigonometric horizontal and vertical components in order to get real and imaginary parts of x + iy (rectangular form).
Consider below example to convert the polar form of complex number 4 ∠300 in to rectangular form.
The vector components are equal to real part and imaginary part of the complex number x + iy. Therefore,
x = A cos θ and y = A sin θ
Let 4 ∠300 = x + iy
4 ∠300 = (4 cos θ) + i (4 sin θ)
= (4 cos 300) + i (4 sin 300)
= (4 x 0.866) + I (4 x 0.5)
= 3.464 + i2
Therefore, the complex number in polar form 4 ∠300 is equal to Z = 3.464 + i2.
Conversions of Rectangular Form to Polar Form, (R→P)
The conversion of rectangular to polar form involves in the use of Pythagoras’s theorem of right angle triangle, formed by the complex number x + iy with the horizontal and vertical axes, in coordinate plane.
Consider the example to convert a rectangular form of complex number 3.464 + i2 into equivalent number in polar form.
Let (3.464 + i2) = A ∠θ
Here A = √(3.462+22 ) = 3.99 (approx 4)
And θ= tan(-1) 2⁄3.46 = 300
Therefore, the complex number in rectangular form Z = 3.464 + i2 is equal to 4 ∠300 in polar form.
Polar Form Multiplication
The easiest way of performing addition and subtraction of complex numbers is rectangular form while polar form is easiest method performing multiplication and division of the complex numbers.
To perform multiplication of polar formed complex numbers, first multiply their magnitudes and then add their angles.
If Z1 and Z2 are the two complex numbers in (polar form), as Z1 = A1 ∠θ1 and Z2 = A2 ∠θ2. Then the multiplication of these two numbers will be
Z1 x Z2 = ( A1 x A2 ) ∠ θ1 + ∠ θ2
Ex: Suppose two complex numbers 2 ∠600 and 5 ∠450, then its multiplication is given as
Z1 = 2 ∠600 and Z2 = 5 ∠450
Z1 x Z2 = (A1 x A2 ) ∠ θ1 + ∠ θ2
= (2 x 5) ∠600 + 450.
= 10 ∠1050
Polar Form Division
To perform the division operation of polar numbers, first divide the magnitudes of the two polars and then subtract the angles.
(Z1 )/Z2 = (A1 /A2 ) ∠ θ1 – ∠ θ2
Suppose two complex numbers are 2 ∠600 and 4 ∠300 then its division is given as
Z1 = 2 ∠600 Z2 = 4 ∠300
(Z1 )/Z2 = (A1 /A2 ) ∠ θ1 – ∠ θ2
= (2 /4 ) ∠ 600 – ∠ 300
= 0.5 ∠ 300
Complex Numbers Using Exponential Form
Apart from Rectangular form (a + ib ) or Polar form ( A ∠±θ ) representation of complex numbers, there is another way to represent the complex numbers that is Exponential form.
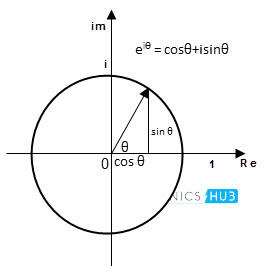
This is similar to that of polar form representation which involves in representing the complex number by its magnitude and phase angle, but with base of exponential function e, where e = 2.718 281. The exponential form of a complex number uses Euler’s formula, eiθ = cos θ + j sin θ.
The general representation of a complex number in exponential form is given as
Z= A e0iθ
Where θ is in radians
This method represents the complex number as a rotating point in the Cartesian plane. This exponential form uses the trigonometric functions or vector components (sine and cosine) of a complex number x + iy. The rotating phasor diagram in Cartesian plane according to Euler’s identity is shown below.
We can represent any complex number by Euler’s method. The Euler’s identity allows us to convert the complex number from exponential form into polar form & to rectangular form.
The relation between polar, rectangular and exponential form is given below.
Z = x + iy= A∠θ= A ( cos θ+isinθ )