As we have seen in previous articles, for simplifying the circuits we used series and parallel combination of resistors to reduce the circuit complexity. In addition, to these we often use source transformation methods to analyse the circuit. But these techniques are not applicable for all types of networks.
Many circuits consist of three terminal networks such as Wye (Y) or star or tee (T) and delta or pi networks. These networks are part of a large network or occur by themselves. The application areas of these networks include three phase networks, matching networks and electrical filters, etc. These networks are simplified using another useful technique called star-delta transformations.
Outline
ToggleStar and Delta Networks
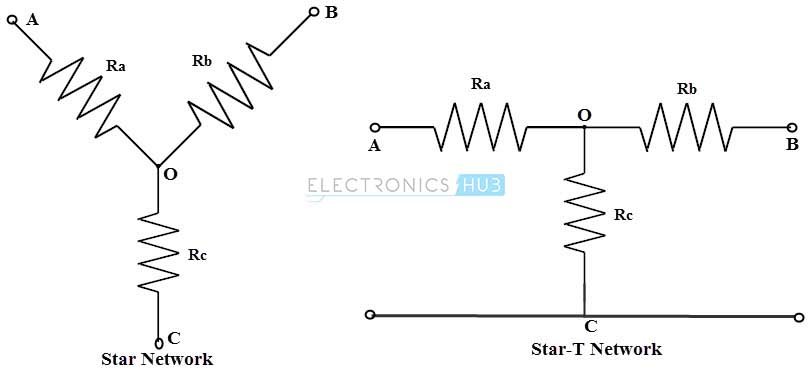
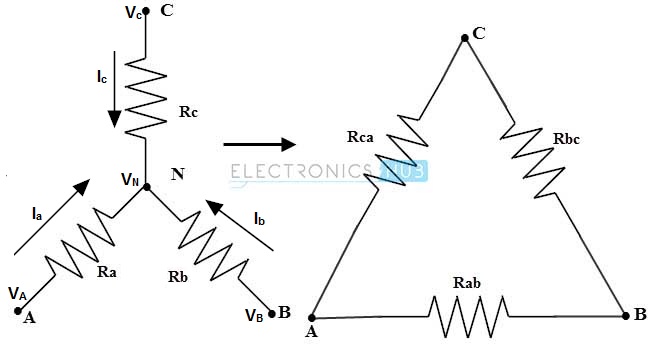
In star connection, components are connected in such a way that one end of all the resistors or components are connected to a common point. By the arrangement of three resistors , this star network looks like a alphabet Y hence , this network is also called as Wye or Y network. The equivalent of this star connection can be redrawn as T network (as a four terminal network) as shown in below figure. Most of the electrical circuits constitute this T form network.
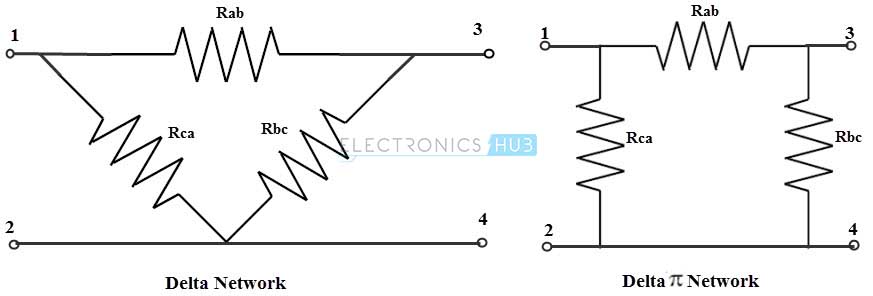
In a delta connection, end point of each component or coil is connected to the start point of another component or coil. It is a series connection of three components that are connected to form a triangle. The name indicates that connection look like an alphabet delta (Δ). The equivalent delta network can be redrawn , to look like a symbol Pi (or four terminal network ) as shown in figure. So this network can also be referred as Pi network.
Delta to Star Transformation
The conversion from star- delta or delta-star can be achieved , when the similar pairs of terminals have the same impedance. This transformation produces a equivalent network by eliminating the node.
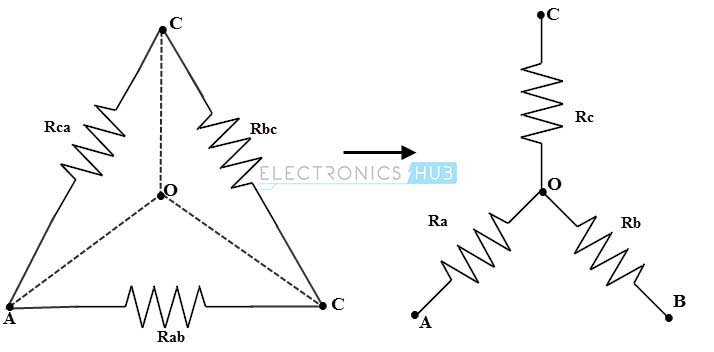
Let us discuss the conversion of delta to star. Consider that Rab, Rbc and Rca are the three series resistances in the delta network and Ra and Rb and Rc are the three resistances in a star network.
This equivalent star network produced after transformation and delta network will have same resistance , when measured between the similar pairs of terminals .
Consider the above figure , where the equivalent resistance between terminals a and c is
Ra+ Rc = Rca ||(Rab + Rbc )
Ra+ Rc = Rca * (Rab + Rbc)/(Rab + Rbc + Rca) ……………………(1)
The equivalent resistance between terminals c and b is
Rb+ Rc= Rbc || (Rab + Rca)
Rb+ Rc = Rbc * (Rab + Rca)/(Rab + Rbc + Rca) …………………….(2)
And between terminals b and a is
Rb+ Ra = Rab ||(Rca + Rbc )
Rb+ Ra = Rab * (Rca + Rbc)/(Rab + Rbc + Rca) ……………………..(3)
By combining above 1, 2 and 3 equations we get
Ra + Rb + Rc = (RabRbc + RbcRca + RcaRab)/(Rab + Rbc + Rca) ……………(4)
By subtracting the equation 2 from equation 4 we get
Ra = (Rab Rca)/(Rab + Rbc + Rca)
Subtracting equation 1 from equation 4 we get
Rb = (Rab Rbc)/(Rab + Rbc + Rca)
And subtracting equation 3 from equation 4 we get
Rc = (Rbc Rca)/(Rab + Rbc + Rca)
These Ra, Rb and Rc are the three resistance values in star network converted from delta equivalent circuit.
Ra = (Rab Rca)/(Rab + Rbc + Rca)
Rb = (Rab Rbc)/(Rab + Rbc + Rca)
Rc = (Rbc Rca)/(Rab + Rbc + Rca)
By observing the above three equations we can say that for a given terminal the equivalent resistance in the star network is equal to the product of two resistances (in the delta) connected to the same terminal divided by the sum of total resistances in the delta network.
Example:
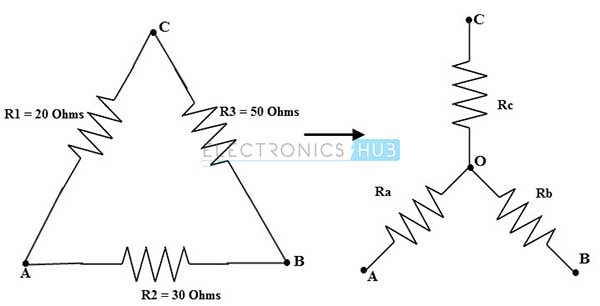
Consider the below figure to transform delta to star or Wye circuit where the values Ra = 20 ohms, R2 = 30 ohms and R3 = 50 ohms.
For delta to star conversions equivalent resistance equations (for this problem) are
Ra = (R1 R2)/(R1 + R2 + R3)
Rb = (R2 R3)/(R1 + R2 + R3)
Rc = (R1 R3)/(R1 + R2 + R3)
Therefore the total resistance, Rt = (R1 + R2 + R3)
= 20 + 30 + 50
= 100 ohms
Ra = (R1 R2)/(R1 + R2 + R3)
= (20 X 30) /100
= 6 ohms
similarly Rb = (R2 R3)/(R1 + R2 + R3)
= (30 X 50) /100
= 15 ohms
and Rc = (R1 R3)/(R1 + R2 + R3)
= (50 X 20)/ 100
= 10 ohms
Star to Delta Transformation
Use the same representation of resistances for the star as Ra, Rb and RC and for delta as Rab, Rbc and Rca. Consider the star network of resistors shown below, where current through Ra resistor is given as
Ia = (Va – Vn) / Ra ………..(1)
By applying KCL at node N in star network then we get
(Va – Vn) /Ra + (Vb – Vn) /Rb + (Vc – Vn) /Rc
Vn [(1/Ra) + (1/Rb) + (1/Rc)] = (Va/Ra) + (Vb/Rb) + (Vc/Rc)
Vn = [(Va/Ra) + (Vb/Rb) + (Vc/Rc)] / [(1/Ra) + (1/Rb) + (1/Rc)] ……(2)
In delta network current at point A is
Ia = (Vab /Rab) + (Vac / Rac) ……(3)
From equations 1 and 3 we get
(Va – Vn) / Ra = (Vab /Rab) + (Vac / Rac) ……………………..(4)
Substituting Vn value from equation 2 in the equation 4 and by simplification we get
Rab = Ra + Rb + ((RaRb)/Rc)
Rac = Ra + Rc + ((RaRc)/Rb)
Similarly Ib in star network is
Ib = (Vb – Vn) / Rb ………..(5)
In delta network
Ib = (Vbc /Rbc) + (Vba / Rba) …………………(6)
By equating 5 and 6 equations
(Vb – Vn) / Rb = (Vbc /Rbc) + (Vba / Rba) ………………..(7)
By substituting equation 2 in the equation 7 and after simplification we get
Rbc = Rb + Rc + ((RbRc)/Ra)
Hence the equations required to transform delta network to equivalent star or wye network are
Rab = Ra + Rb + ((RaRb)/Rc) = ( RaRb + RbRc + RbRc )/Rc
Rbc = Rb + Rc + ((RbRc)/Ra) = ( RaRb + RbRc + RbRc )/Ra
Rac = Ra + Rc + ((RaRc)/Rb) = ( RaRb + RbRc + RbRc )/Rb
By observing the above three equations we can say that between the given two terminals the equivalent delta resistance is equal to the sum of two resistances (in the star) connected to those terminals plus the product of the same two resistances divided by remained or third star resistance.
Example:
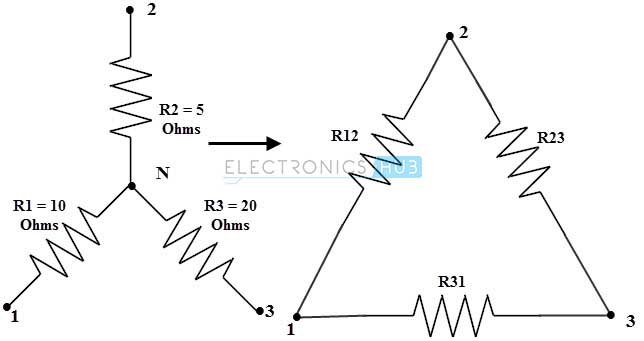
Consider the below figure to transform star or Wye to the delta circuit where the resistance values in star network are given as R1= 10 ohms, R2= 5 ohms and R3 = 20 ohms.
For star or wye to delta conversion, the equivalent resistance equations (for this problem) are
R12 = R1 + R2 + ((R1R2)/R3)
R23 = R2 + R3 + ((R2R3)/R1)
R31 = R1 + R3 + ((R1R3)/R2)
By simplifying the above equations we get the common numerator term as
R1R2 + R2R3 + R1R3
= 10 X 5 + 10 X 20 + 20 X 5
= 350 ohms
Then R12 = 350/ R3
= 350/20
= 17.5 ohms
R23 = 350/ R1
= 350/ 10
= 35 ohms
R31= 350/R2
= 350 /5
= 70 ohms