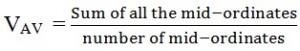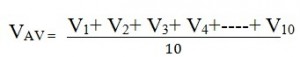Calculating the magnitude of alternating quantities like current or voltage in AC is not a straight forward job as in DC where the values are constant over time. There are several methods to represent the magnitude of an Alternating waveform. In case of an AC sinusoidal waveform, the magnitudes of voltage and current can be represented by
- Peak value
- Peak – to – Peak value
- RMS value
- Instantaneous value
(These values can be used to represent the magnitude of even any other periodic waveform)
There is another way to represent the magnitude of an AC waveform. It is known as Average value.
The values of average voltage and average current of an AC sine wave can be useful in many circuit analysis operations. In fact, rectifier type multi-meters measure the average voltage of the AC and then perform some calculations on that and display the output as RMS value.
What Is Average Value of an AC Wave?
The average value of an AC wave, specifically for a sinusoidal wave, refers to the arithmetic mean of the waveform over one complete cycle. It’s calculated by integrating the area under the curve of one cycle and dividing by the cycle’s period. For a pure sine wave, the average value over a full cycle is zero, due to the equal areas above and below the zero axis. However, for half-wave rectified signals, the average value is positive, representing the net area under the curve.
Average Voltage
Average voltage, as the name indicates, is the average of instantaneous voltages that are chosen at appropriately timed intervals in the half cycle of an AC sinusoidal (or any other periodic) waveform. Average value represents the quotient of the area under AC wave form with respect to time.
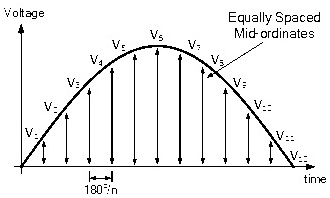
To find the average voltage of an alternating wave form, one half cycle is divided into equally spaced ordinates. The instantaneous voltages at these mid-ordinates is calculated. By calculating the average value of these instantaneous voltage values, we get the average value of an AC waveform (whether voltage or current).
Determining the average voltage value of an AC waveform is similar to finding the RMS voltage of the alternating waveform. But in the process of finding the average voltage, there is no need to find the squares of the instantaneous voltages. We can find the average voltage value of any shaped of wave form.
The average voltage value can be said as “The quotient of the area under the curve (either sine wave or square wave or any other periodic wave) at any instance of time” or we can also say “The average of all instantaneous voltage values is known as Average voltage”.
Every periodical wave form is symmetrical in shape i.e. there will be a positive half cycle and negative half cycle. The area under the positive half cycle is always equal and opposite in sign to that of the area under the negative half cycle.
The sum of the areas under both half cycles is returned to Zero, as the negative and positive areas cancel each. Hence, the average value is calculated by considering only half the period.
The average voltage value is measured only over one half cycle of the complete periodic waveform. The average voltage is also called as the “Mean voltage of waveform”.
The mean value can be found for both AC and DC circuit analysis and calculations. Average value is represented by VAVG for average voltage and IAVG for average current.
The Concept of Instantaneous Value
Instantaneous value (either voltage or current) of an alternating waveform is the value at any particular instant of time. The voltage of a waveform at a given instant in time is called “Instantaneous voltage”.
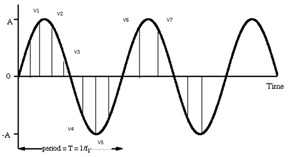
In the above diagram V1, V2, V3, V4 … are the instantaneous voltages of the sine wave. To find the instantaneous voltage value of a sinusoidal wave, we depend on maximum voltage of the sine wave.
Instantaneous voltage = Maximum voltage x sin θ
VINST = VMAX x sin θ
Here, θ is the angle at which the mid-ordinates are made. For example, in case of an AC sinusoidal wave, the maximum angle is 1800 for positive half cycle. If we divide the half cycle into 10 mid-ordinates, then θ will be multiples of 1800 / 10 = 180 i.e. θ takes 180, 360, 540….up to 1800.
Average Voltage of a Waveform in Graphical Method
The average value of an alternating waveform like sinusoidal wave, when taken for a full cycle, is equal to 0. This is because, a sinusoidal waveform, which is an alternating wave i.e. it is symmetric over X-axis and the values in positive half cancels the values in negative half when an average is taken.
But the average values of sinusoidal voltages and currents cannot be 0 in real time. Hence, the average value of an alternating value can be calculated by taking the averages of the equally spaced instantaneous values of the half cycle of an alternating waveform.
This process is similar to the process of finding the RMS voltage. The positive half cycle is equally divided into n number of portions with equal spaces between them. The equally divided portions are called “Mid ordinates” and this quotient value of each portion is called “Instantaneous value”.
Each mid ordinate value of an alternating waveform is added to its next ordinate’s value and the added total is divided by total number of mid ordinates. This is the value of the average voltage. The average voltage is given by the below represented formula.
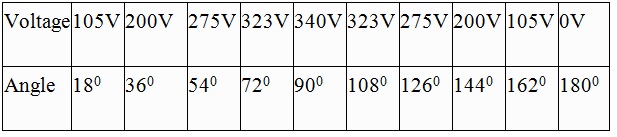
For example, if we have divided the half cycle into 10 equal ordinates, then the average voltage can be calculated as
If we consider an alternating wave representing an AC voltage with the maximum voltage as 340v, then the average voltage can be calculated as follows.
Divide the curve into 10 mid-ordinates and calculate the instantaneous voltages at those points.
Using the above formula, the average voltage can be calculated as
Vavg = 2146 / 10 = 214.6 volts
Therefore, the average voltage value is 214.6 volts.
Average Voltage of a Waveform in Analytical Method
As we already know, every periodical waveform has its average value as a sum of zero as it has the equal portions of positive and negative half cycles. The average value can be calculated by considering the instantaneous value of only a half cycle instead of all the instantaneous values.
This is applicable only to symmetrical waveforms like sinusoidal waves. In non-symmetrical voltages, we should calculate the average of the instantaneous voltages for the complete cycle of the periodic waveform, in order to find the accurate value.
Approximation of the Area
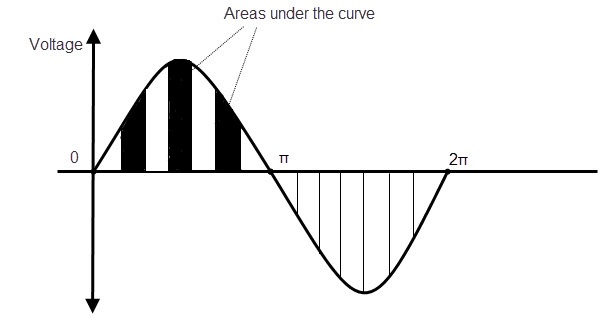
In order to find the average value, we need to calculate the approximate area of the waveform or curve at several intervals. In order to find the area of the curve, it is divided into many small rectangles or triangles. By approximating the areas of these individual rectangles, and adding all these areas, the average value can be calculated.
The accuracy of the average value can be increased by considering an infinite (very large) number of small rectangles. The following graph represents the average of the area covered under the curve with small rectangles at equal intervals of the waveform.
By calculating the average of the area under the curve, we can find the exact value of the average voltage value. The most accurate value will be occurred when the value approaches 2Π.
There are many methods to approximate the value of the area under the curve. They are Trapezoidal rule, mid – ordinate rule, Simpson’s rule, etc. If we consider an AC voltage sine wave, it is represented as V (t) = Vp.cos (ωt). The area under the curve at every instance is mathematically given as
Area = VpSin(wt)dt
Here, T is the time period of the periodic waveform and the limits of the integration are 0 and Π as we are considering only the half cycle.
Using the above formula, we can calculate the area under the waveform and we get that as
Area = 2VP.
Now, we know the area under the positive half cycle (or negative half cycle), we can easily calculate the average value (voltage or current) of the periodic alternating sinusoidal wave by integrating the sine quantity over positive (or negative) cycle and dividing it with the period.
For example, if we have the instantaneous voltage of the alternating wave as V = Vp.sinθ with the time period 2Π then the average voltage of the AC wave form is
VAV=1/Π VpSin(Φ)dΦ
VAV=Vp/Π -cos(Φ)
=2Vp/Π = 0.673Vp
Average Voltage Equation
The average voltage value of an alternating waveform is given by
VAV=2Vp/Π = 0.673Vp
So the average value of the AC sinusoidal wave is equal to the multiplication of peak voltage value with 0.637.
As the above discussed example, if we have a sine wave with 340 Volts maximum (peak) voltage, then the average voltage value can be found in analytical method is given below.
VAV = VPEAK x 0.637 = 340 x 0.637 = 216.5 V.
The value of RMS voltage in terms of peak voltage is VRMS = 0.707 x VPEAK. Comparison of average and RMS voltage is shown below.
NOTE: Multiplying the peak value with 0.637 is only applicable for sine wave, it doesn’t apply for other waveforms like sawtooth wave and triangle wave.
Importance of Average value in AC Sinusoidal Waveform Measurements
Rectifier type multi-meters indicate the RMS values (voltage or current) for sinusoidal waves only. The RMS value is calculated by first calculating the Average value and then multiplying by 1.11. If we use this multi-meter for measurement of RMS value of any other Alternating waveforms, the result will be an erroneous RMS value.
Summary
- The waveform which changes its direction periodically is known as “Alternating waveform” or “AC waveform”.
- The procedures of finding the RMS value and the average values of an alternating waveform are similar.
- We calculate the average value by considering only the half cycle of an alternating waveform.
- There are two methods for calculating the average value of the AC waveform or an alternating waveform. They are
1. Analytical method
2. Graphical method
- For graphical method, the formula for finding the average voltage is
- For analytical method, the formula for average voltage value is
- The relation between the average voltage and the maximum voltage value or peak voltage value is given as “Average voltage is 0.637 times the peak voltage”.
VAVG = VPEAK x 0.637